Capítulo 3 Clasificación con KNN
3.1 Carga de dataset y exploración
Como es habitual el internet de las cosas industriales amenudo puede generar datos que van cambiando minuto a minuto. Por ello se hace necesario tener un mecanismo para tomarlos desde la fuente que lo genera en forma inmediata, cada vez que querramos realizar un reporte automático o análisis exploratorio del mismo.
library(readr)
performance_scm <- read_delim("https://themys.sid.uncu.edu.ar/rpalma/R-cran/scm_perform.csv", delim = ";", escape_double = FALSE, col_types = cols(Performance = col_factor(levels = c("good", "fair", "poor"))), locale = locale(decimal_mark = ",", grouping_mark = "."), trim_ws = TRUE)Carga de Bibliotecas Utilizadas
library(e1071) # svm navie bayes
library(class) # knn
library(caret) # Construcción de Modelos
#> Loading required package: ggplot2
#> Loading required package: lattice
library(neuralnet) # Redes Neuronales
library(randomForest) # Random Forest
#> randomForest 4.7-1.1
#> Type rfNews() to see new features/changes/bug fixes.
#>
#> Attaching package: 'randomForest'
#> The following object is masked from 'package:ggplot2':
#>
#> margin
library(ggplot2) # Representacion del conocimiento
library(gridExtra) # Ploteo
#>
#> Attaching package: 'gridExtra'
#> The following object is masked from 'package:randomForest':
#>
#> combine3.2 Entrenamiento y prueba
Separaremos los datos en dos conjuntos aleatorios
- Dataset de Entrenamiento
- Dataset de Prueba
Los datos puede ser elegidos aleatoriamente con el comando sample. En nuestro caso emplearemos la proporción \(70/30\) 70% Para entrenar 30% para test (preuba). Esto debería dejaronos 105 observaciones en un conjunto y 45 en el otro.
Para que podamos repetir el experimento con los mismos datos fijaremos la semilla y así obtener resultado parecidos.5
set.seed(831)
inTrain.C <- createDataPartition(performance_scm$Performance,p=.7,list = FALSE)Ahora partiremos el dataset utilizando como índice inTrain.C
training.C <- performance_scm[inTrain.C, ]
testing.C <- performance_scm[-inTrain.C, ]Podemos ver la tabla de resultados contenidos con este comando
table(training.C$Performance)
#>
#> good fair poor
#> 35 35 35Del mismo modo podemos ver el dataset de pruebas
table(testing.C$Performance)
#>
#> good fair poor
#> 15 15 153.3 Ajuste del modelo
Realizaremos una tabla de contingencia o matriz de confusión
| Actual + | Actual - | |
|---|---|---|
| Predic + | True Positivo | False Positivo |
| Predic - | False Positivo | True Negativo |
3.4 Mediciones Model-level
3.4.1 Accuracy
Mide la proporción de predicciones correctas y no es extraño encontrarlo como porcentaje. Su rango va de 0 a 100% . A valor más alto mejor preformance del modelo.6
\[Accuracy = \frac {TP + TN}{TP+TN+FP+FN} \]
3.5 Class-Level Mesures
3.5.1 Precisión
Mide cuantas predicciones hechas fueron correctas respecto del total de predicciones emitidas.
\[Precision = \frac{CorrectPredic}{TotalPredic}\]
3.5.2 Recall o rememoración
Estima cuantas predicciones para una clase dada son correctas contra el total de casos predichos en la clase (entrenamiento y test)
\[Recall = \frac{CorrectPredic}{TotalActual}\] ### Métrica-F Estima la bondad de clasificación para una clase dada. Se compara el total de casos correctamente clasificados contra el balance en la precisión y rememoración (recall). El valor máximo de F-Messure es igual a 1
\[F1Messure = 2*\frac{Precision * Recall}{Precision * Recall} \]
3.7 k Nearest Neighbor kNN
En kNN la similaridd o distancia entre observaciones es utilizada para clasificar los elementos de una muestra o población. Tipicamente usamos la distancia Euclídea en el espacio n dimensional. El modo más común de clasificación de un grupo es con el k-ésimo vecino(s) más próximo(s) en base a datos etiquetados.7
Se dice que kNN es una instanciación antes que un método basado en modelo, significando esto que en realidad no se crea un modelo para clasificar.
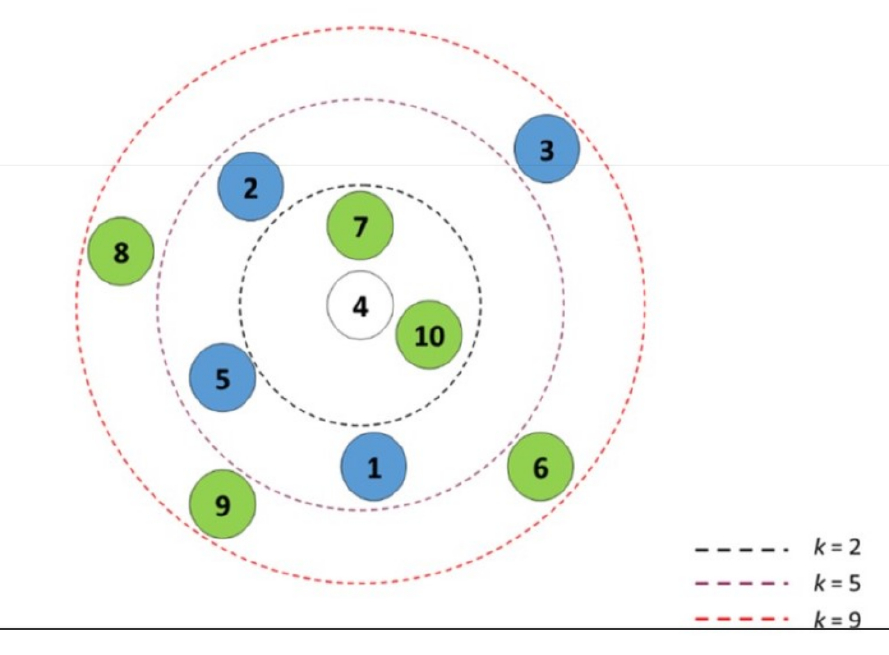
Eligiendo un k grande, se reduce el impacto de la varianza causada por el “ruido” aleatorio de los datos, pero esto puede sesgar el aprendizaje de ignorar patrones pequeños, pero significativos.
Se suele utilizar una regla de facto para elegir k, que es la raíz cuadrada del número de observaciones del set de entrenamiento redondeado hacia arriba
\[k =\sqrt{n_{training}}\]
Para el dataset de performance logística se tiene
Utilizar un número impar para \(k\) es una buena práctica, porque evita caer en empate al seleccionar la etiqueta dominante.
Utilizaremos la función \(knn()\) del paquete \(class\) para construir lo que representaría el modelo.
library(class)
knn.pred.C <- knn(train=training.C[ ,1:4] , test=testing.C[ , 1:4], cl=training.C$Performance, k=k.choice)3.7.1 Testeo de Performace del Algoritmo entrenado
Dado que kNN no precide un modelo no podemos hacer una ponderación o medida de la bondad del ajuste en los datos de entrenamiento, por lo que debemos necesariamente aplicar el modelo a los datos de prueba.8
knn.test.acc <- confusionMatrix(knn.pred.C,testing.C$Performance, mode="prec_recall")
knn.test.acc
#> Confusion Matrix and Statistics
#>
#> Reference
#> Prediction good fair poor
#> good 15 0 0
#> fair 0 14 0
#> poor 0 1 15
#>
#> Overall Statistics
#>
#> Accuracy : 0.9778
#> 95% CI : (0.8823, 0.9994)
#> No Information Rate : 0.3333
#> P-Value [Acc > NIR] : < 2.2e-16
#>
#> Kappa : 0.9667
#>
#> Mcnemar's Test P-Value : NA
#>
#> Statistics by Class:
#>
#> Class: good Class: fair Class: poor
#> Precision 1.0000 1.0000 0.9375
#> Recall 1.0000 0.9333 1.0000
#> F1 1.0000 0.9655 0.9677
#> Prevalence 0.3333 0.3333 0.3333
#> Detection Rate 0.3333 0.3111 0.3333
#> Detection Prevalence 0.3333 0.3111 0.3556
#> Balanced Accuracy 1.0000 0.9667 0.98333.8 Buenas prácticas en kNN
- Normalizar los valores
Dado que kNN se basa en las distancias puede haber un error de influencia si una columna tiene magnitudes muy diferentes a otra.9
boxplot(performance_scm[ ,1:4])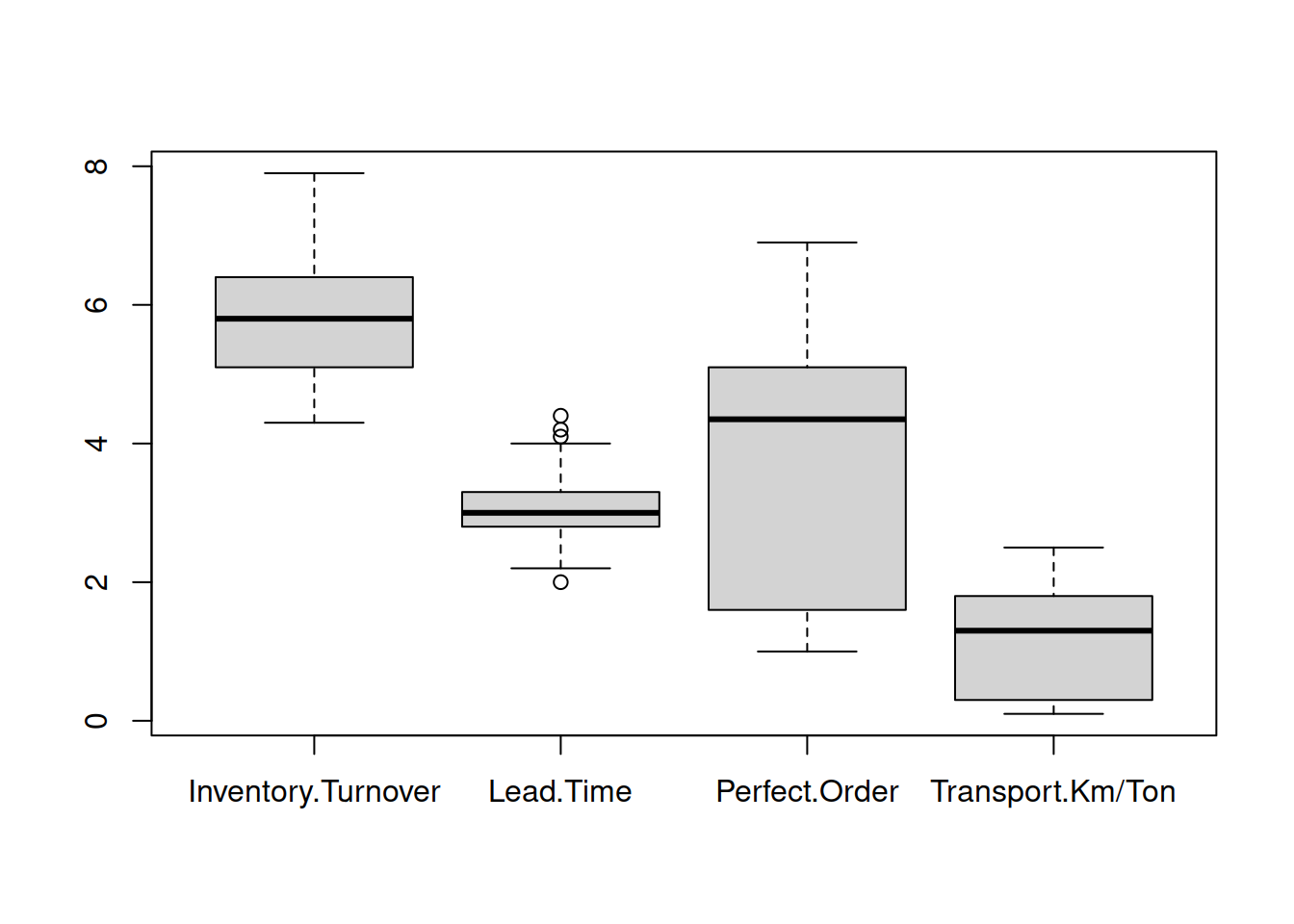
Basados en el gráfico boxplot deberíamos transfomar el recorrido de las variables al rango \([0,1]\).
\[ \frac{x-min(x)}{max(x)-min(x)}\] Noramlizaremos los datos
perf_escalado <-apply(performance_scm[ ,1:4], 2, function (x) (x-min(x))/(max(x)-min(x)) )
perf_escalado <- data.frame(perf_escalado, performance_scm$Performance)Ahora podemos hacer el gráfico con los valores escalados
boxplot(perf_escalado[ ,1:4], main="Gráfico de cajas Predictores Escalados", las=2)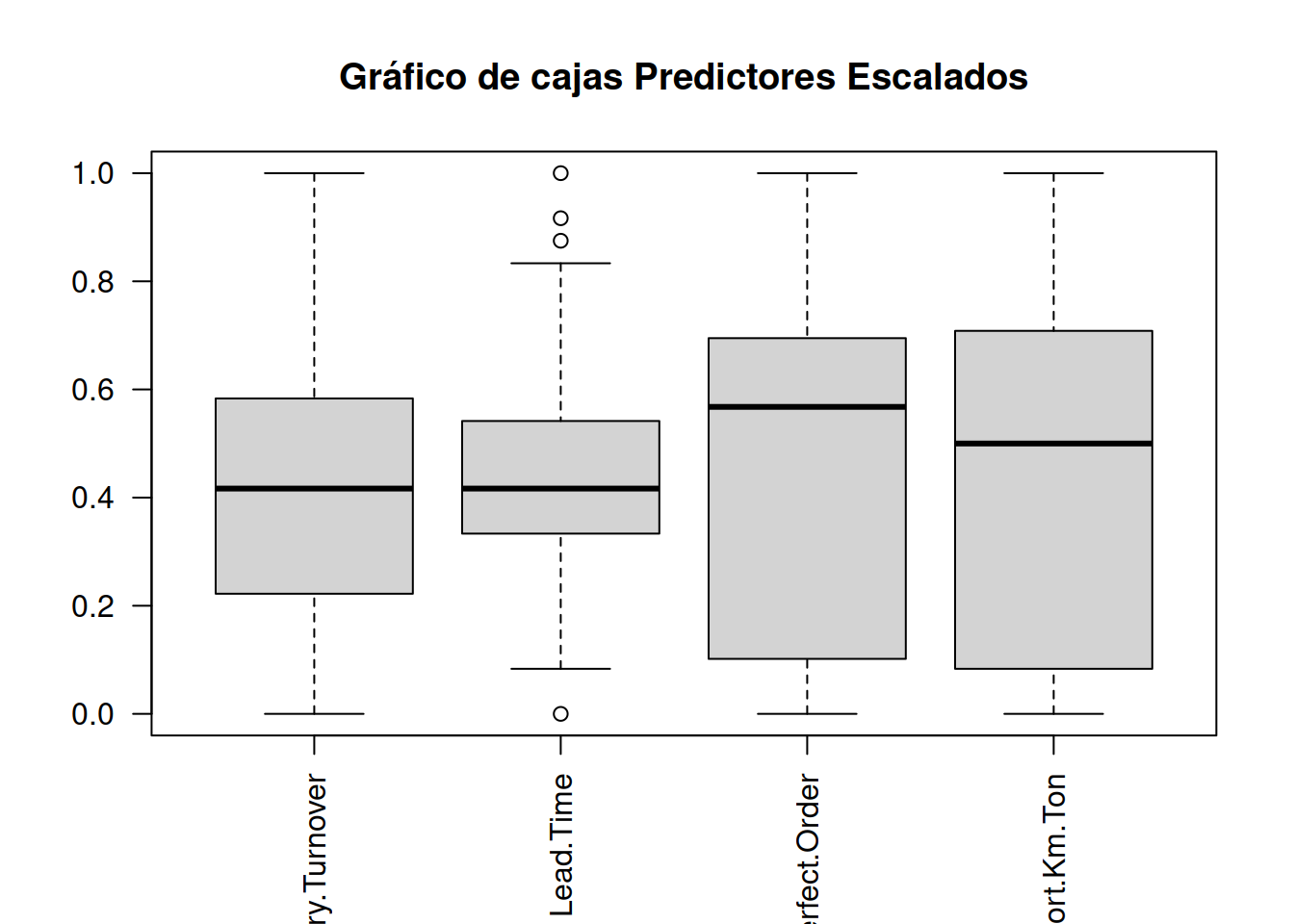
Alternativamente de puede usar z-scores, que están estandarizados con la media entorno a 0 y el desvío estandard.
\[Z= \frac{x-u}{\sigma} \]
perf_z <- apply(performance_scm[ ,1:4],2, function(x) (x-mean(x)) / (sd(x)) )
perf_z <- data.frame(perf_z,performance_scm$Performance)Vista del gráfico normalizado
boxplot(perf_z[ ,1:4])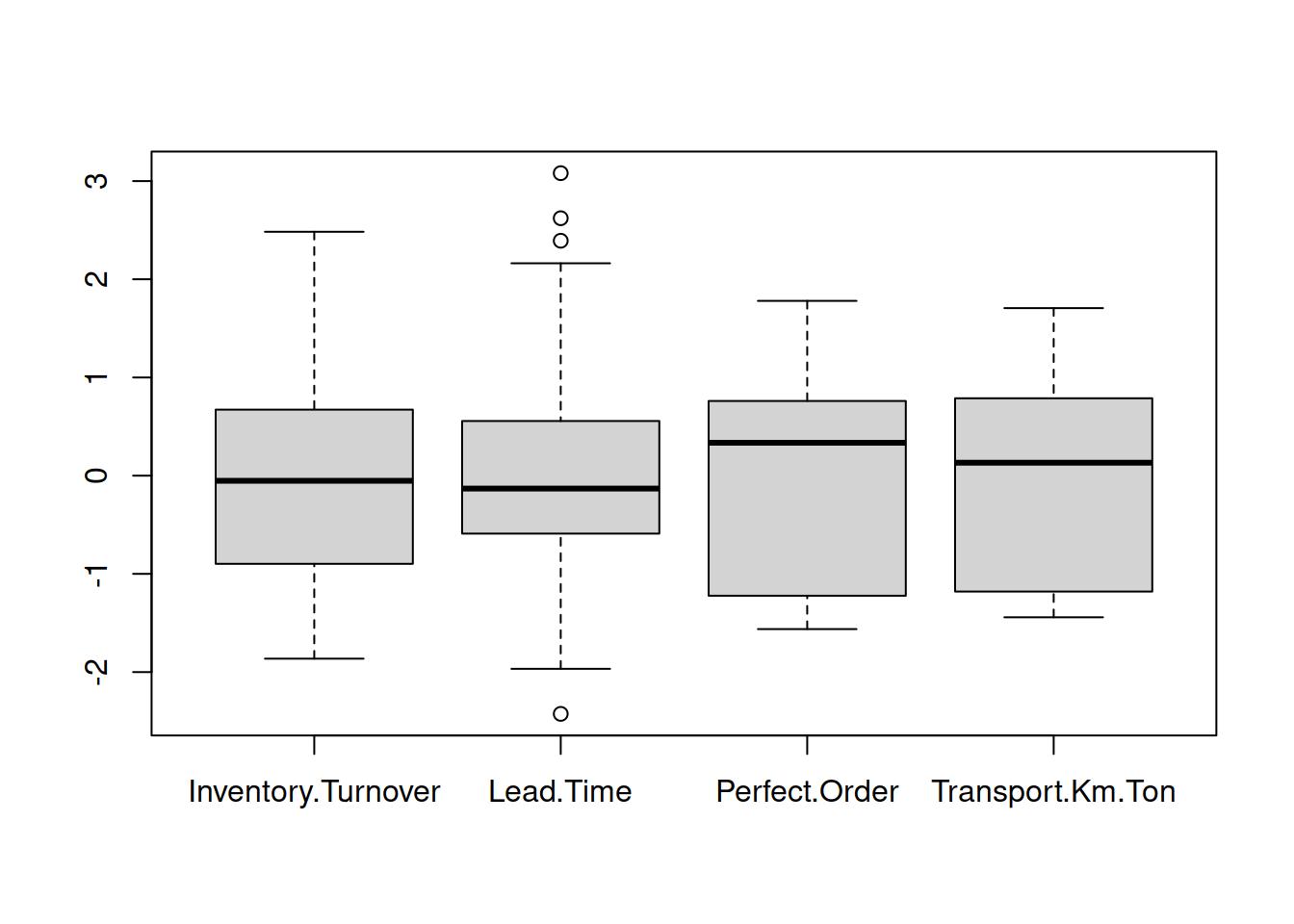
3.9 Evaitar sobre entrenamiento
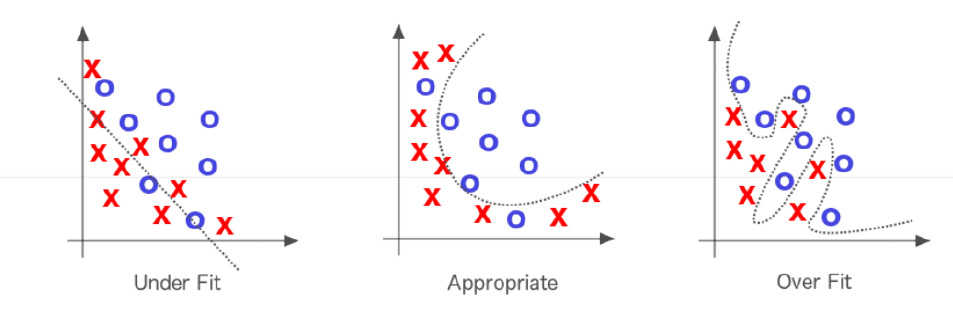
3.9.1 Variando k
Dado que kNN es un algoritmo de aprendizaje peresozo, pero eficiente a la hora de hacer predicciones (pues en realidad no hay aprendizaje formal), resulta interesante probar el efecto de variar los valores de k y ver cómo impacta en los resultados obtenidos y la performance de entrenamiento.
save <- list()
for (i in 1:25){
knn.pred.C.l <- knn(train = training.C[ ,1:4], test=testing.C[ ,1:4], cl=training.C$Performance, k=i)
save[[i]] <-confusionMatrix(knn.pred.C.l, testing.C$Performance, mode="prec_recall")$overall[1]
}
save <-do.call(rbind,save)
plot(1:25,save, xlab="k", ylab="Accuracy", type="o")