Capítulo 1 Bases Estadística
1.3 Analítica de Datos y Automatización de Procesos
Existen diversas aproximaciones para llegar a entender lo que una serie de paradisgmas emergnetes pueden aportar a cursos como este. Algunos de ellos más antiguos, tales como Minería de Datos, hasta los más recientes como Analítica de Datos o Deep Learning. Todos ellos constituyen un confjunto de definiciones y reglas que poseen una raiz común y partes de la perspectiva estadística para para concluir en la inteligencia artificial
Tratando de expresar una evolución histórica y sin profundizar en los aspectos comunes y en los que difieren podemos pensar en la siguiente evolución histórica de los paradigmas.
- Statistical Learning (Aprendizaje Estadístico)
- Machine Learning (ML)
- Artifical Intelligence
- Data Mining (and Business Intelligence)
- Data Science
1.4 La Recomendación de el IADB
Antes de comenzar con la introducción teórica sería bueno que dialoguemos y aprendamos de quienes, por el puesto que tienen en la gestión de salud, han tenido más oportunidades y experiencia en el terreno de implementar y aplicar estas herramientas en en nuestro campo disciplinar. En tal sentido recomiendo revisar el video del “Cristina Silcox” que como respondable experta en política sanitaria del Banco Interamericano de Desarrollo tiene la posibilidad de compartir con nosotros su enorme experiencia en el uso de IA en la salud de los países de nuestro continente.
Potential and risk of IA in helth
1.5 Flujo de Trabajo
En todas las técnicas que mencionamos antes existen una serie de pasos que se repiten. Son acciones automáticas que se utilizan como receta (que llamaremos scripts) para supervisar y sobre todo entender los resultados que obtenemos y como estos se ven afectados por una serie de hechos y acciones que comienzan con la captura de la información.
Estos pasos que se utilizan consisten en :
- Capturar la información (o generarla por simulación)
- Criterio de eliminación de outailers
- Tratamiento de NA (decidir sobre ello)
- Escalado
- Normalización
- Modelización
- Prueba de Calidad del Modelo
- Utilización desciptiva (exploratoria)
- Utilización predictiva
- Utilización prescriptiva
- Riesgo y error admisible
- Dócima de las hipótesis
Realizaremos un pequeño ejemplo en el que utilizaremos algunos de los paso para entender el flujo de trabajo.
1.5.1 Caso de estudio cancer de próstata
Tenemos una colección de datos que se han reunido de las historias clínicas de los pacientes de un consultorio en la zona rural que es atendido por un médico. La población en cuentión está repartida por un área de 40 Km a la redonda del centro de salud. La principal actividad de la región fue la cria de ganado menor, pero la presión impuesta por la expansión de la frontera de la soja ha impulsado la cría de ganado mayor. Lógicamente para sostener este ganado se ha recurrido al cultivo de pasturas bajo riego artificial y el uso de herbicidas (RoundUp) para el control de malezas.
Se disponen de dos muestras. La primera tomada en 1975 y la segunda en 2018 sobre individuos de diferentes edades y los resultados que arroja el diagnóstico sobre el antígeno prostático. Ante niveles elevados de este marcados y sin poder disponer de más datos se intuye que se puede estar ante un caso positivo de cáncer de próstata. La dificultad en acceder al paciente nos pone en la disyuntiva de ser críticos y adoptar un carácter conservador respecto del diagnóstico preliminar.
La población en 1975 era de 45.000 habitantes (datos del censo de salud) en tanto que en 2018 se había estimado por tratamiento de imágener satelitales que la población ascendía a 123.000.
Captura de datos !
Realizaremos los pasos básicos y no escalaremos ni procesaremos (limpiaremos datos erroneos, corregir errores de tipeo, etc.)
1.5.2 Información base
| Historia clínica 1975 | Edad | Diagnóstico PSA |
|---|---|---|
| 1 | 19 | 0 |
| 2 | 18 | 0 |
| 3 | 22 | 0 |
| 4 | 25 | 0 |
| 5 | 17 | 0 |
| 6 | 30 | 0 |
| 7 | 29 | 0 |
| 8 | 32 | 0 |
| 9 | 31 | 0 |
| 10 | 33 | 0 |
| 11 | 38 | 0 |
| 12 | 36 | 0 |
| 13 | 40 | 1 |
| 14 | 40 | 0 |
| 15 | 42 | 0 |
| 16 | 45 | 0 |
| 17 | 47 | 0 |
| 18 | 49 | 0 |
| 19 | 55 | 0 |
| 20 | 58 | 1 |
| 21 | 57 | 1 |
| 22 | 63 | 1 |
| 23 | 65 | 1 |
| 24 | 65 | 1 |
| 25 | 66 | 1 |
Trucos:
Puedes cargar los datos en un vecto con el comando Edad_75 <- scan() . tipea uno a uno los valores de edad y luego dos veces seguidas Enter para finalizar el proceso.
En los siguientes capítulos veremos como capturar de fuentes de datos como .xls
| Historia clínica 2018 | Edad | Diagnóstico PSA |
|---|---|---|
| 1 | 19 | 0 |
| 2 | 18 | 0 |
| 3 | 22 | 0 |
| 4 | 25 | 0 |
| 5 | 17 | 0 |
| 6 | 30 | 0 |
| 7 | 29 | 0 |
| 8 | 32 | 0 |
| 9 | 31 | 0 |
| 10 | 33 | 0 |
| 11 | 38 | 1 |
| 12 | 36 | 0 |
| 13 | 40 | 1 |
| 14 | 40 | 0 |
| 15 | 42 | 1 |
| 16 | 45 | 0 |
| 17 | 47 | 1 |
| 18 | 49 | 0 |
| 19 | 55 | 0 |
| 20 | 58 | 1 |
| 21 | 57 | 1 |
| 22 | 63 | 1 |
| 23 | 65 | 1 |
| 24 | 65 | 1 |
| 25 | 66 | 1 |
| 26 | 69 | 1 |
| 27 | 70 | 1 |
| 28 | 71 | 1 |
| 29 | 75 | 1 |
| 30 | 86 | 1 |
| 31 | 79 | 1 |
| 32 | 88 | 1 |
| 33 | 89 | 0 |
| 34 | 92 | 1 |
| 35 | 84 | 1 |
1.6 Tratamiento y captura de la información
datos_75 <- c(1 , 19 , 0,
2 , 18 , 0,
3 , 22 , 0,
4 , 25 , 0,
5 , 17 , 0,
6 , 30 , 0,
7 , 29 , 0,
8 , 32 , 0,
9 , 31 , 0,
10, 33 , 0,
11, 38 , 0,
12, 36 , 0,
13, 40 , 1,
14, 40 , 0,
15, 42 , 0,
16, 45 , 0,
17, 47 , 0,
18, 49 , 0,
19, 55 , 0,
20, 58 , 1,
21, 57 , 1,
22, 63 , 1,
23, 65 , 1,
24, 65 , 1,
25, 66 , 1)
Muestra_75 <- matrix(datos_75, ncol = 3, byrow = TRUE)
Muestra_75## [,1] [,2] [,3]
## [1,] 1 19 0
## [2,] 2 18 0
## [3,] 3 22 0
## [4,] 4 25 0
## [5,] 5 17 0
## [6,] 6 30 0
## [7,] 7 29 0
## [8,] 8 32 0
## [9,] 9 31 0
## [10,] 10 33 0
## [11,] 11 38 0
## [12,] 12 36 0
## [13,] 13 40 1
## [14,] 14 40 0
## [15,] 15 42 0
## [16,] 16 45 0
## [17,] 17 47 0
## [18,] 18 49 0
## [19,] 19 55 0
## [20,] 20 58 1
## [21,] 21 57 1
## [22,] 22 63 1
## [23,] 23 65 1
## [24,] 24 65 1
## [25,] 25 66 1Obtener el la edad del paciente de la 3er historia clínica
Muestra_75[3,2]## [1] 22Obtener las edades de la muestra
plot (sort(Muestra_75[ ,2]), main= "Rango Etareo",xlab="Paciente", ylab= "Edad")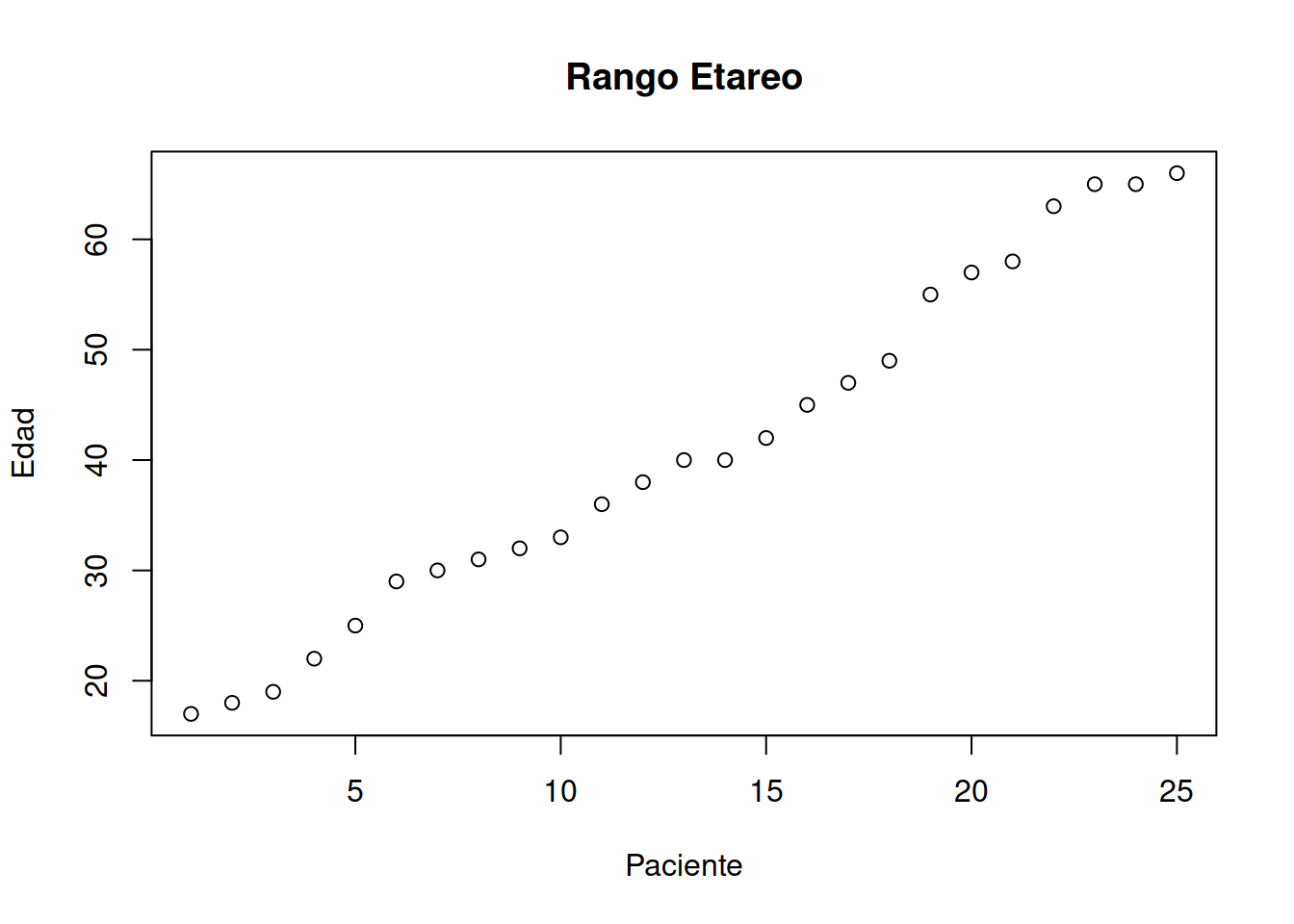 ### Muestra de Historias Clínicas
### Muestra de Historias Clínicas
plot(Muestra_75[ , 1:2],main = "Resumen de Casos",xlab = "Historia Clínica",ylab="Edad", type="b", col="RED")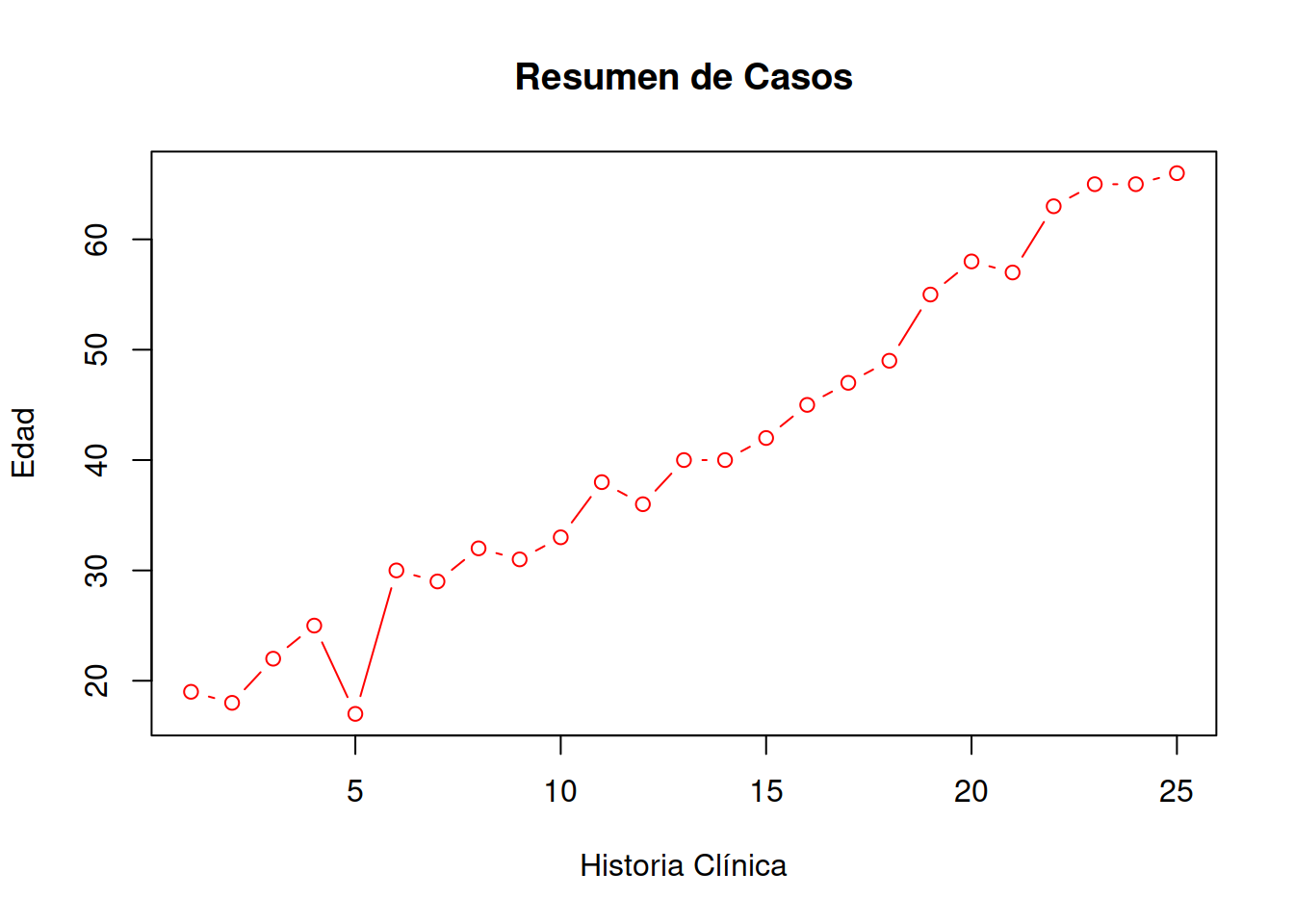
1.8 Gráficos de Densidad
También conocido como gráfico de densidad de Kernel y gráfico de densidad de traza.
Un gráfico de densidad visualiza la distribución de datos en un intervalo o período de tiempo continuo. Este gráfico es una variación de un Histograma que usa el suavizado de cerner para trazar valores, permitiendo distribuciones más suaves al suavizar el ruido. Los picos de un gráfico de densidad ayudan a mostrar dónde los valores se concentran en el intervalo.
Una ventaja de los gráficos de densidad sobre los histogramas es que son mejores para determinar la forma de distribución porque no se ven afectados por el número de contenedores utilizados (cada barra utilizada en un histograma típico). Un histograma que consta de solo 4 compartimientos no producirá una forma de distribución lo suficientemente distinguible como lo haría un histograma de 20 compartimientos. Sin embargo, con los gráficos de densidad esto no es un problema.
La función de densidad puede calcularse fácilmene en R-Cran con el siguiente comando
density(Muestra_75[ ,2])##
## Call:
## density.default(x = Muestra_75[, 2])
##
## Data: Muestra_75[, 2] (25 obs.); Bandwidth 'bw' = 7.394
##
## x y
## Min. :-5.183 Min. :5.383e-05
## 1st Qu.:18.159 1st Qu.:2.474e-03
## Median :41.500 Median :1.246e-02
## Mean :41.500 Mean :1.070e-02
## 3rd Qu.:64.841 3rd Qu.:1.698e-02
## Max. :88.183 Max. :2.186e-02Dado que es un objeto de R a partir del resultado de los cuantiles es posible plotear directamente la función invocada
plot(density(Muestra_75[ ,2]), main = "Gráfico de Densidad", ylab="Cantidad relativa de muestras",xlab="Edad")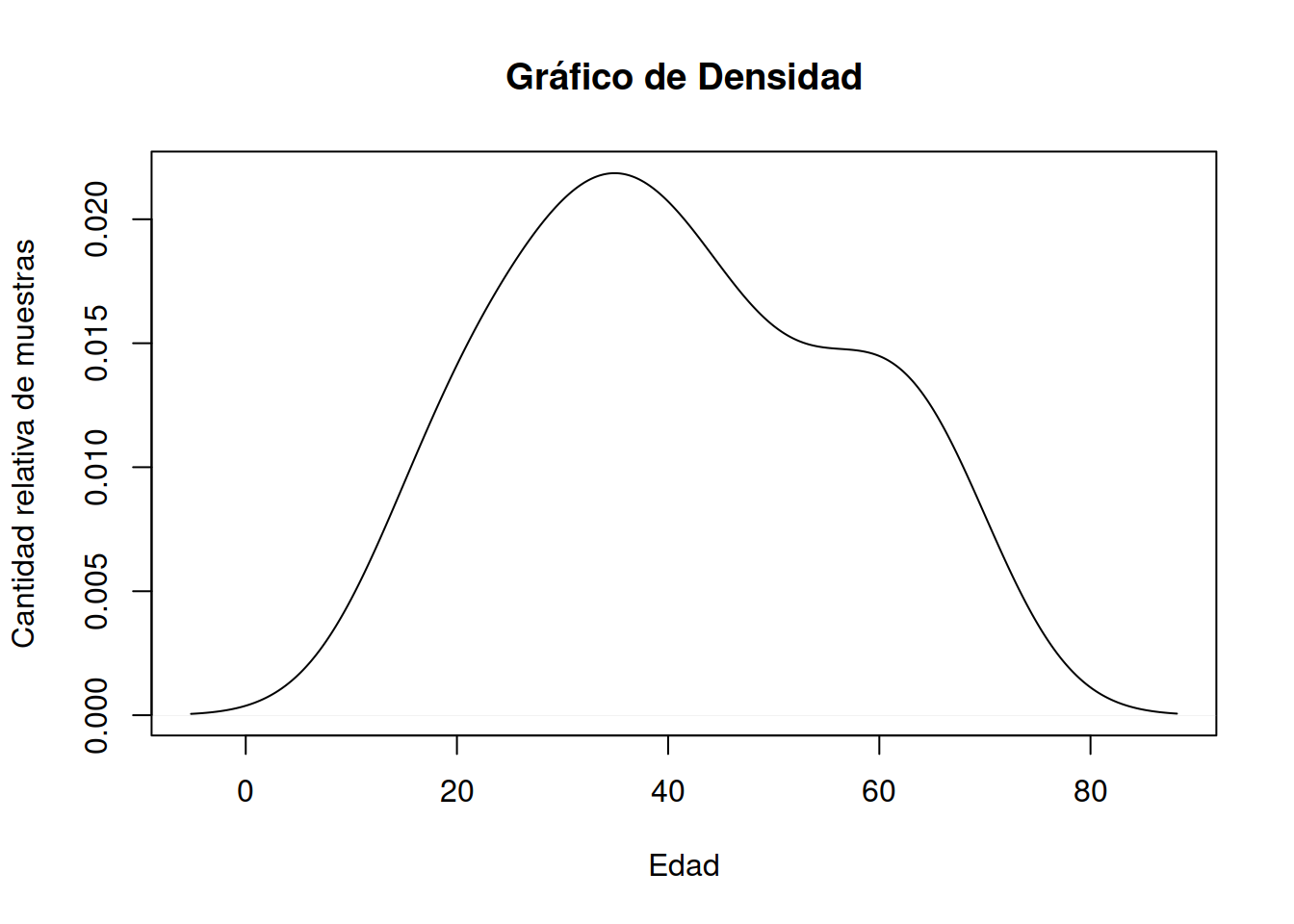
1.8.1 Gráfica conjunta de Histograma y Densidad
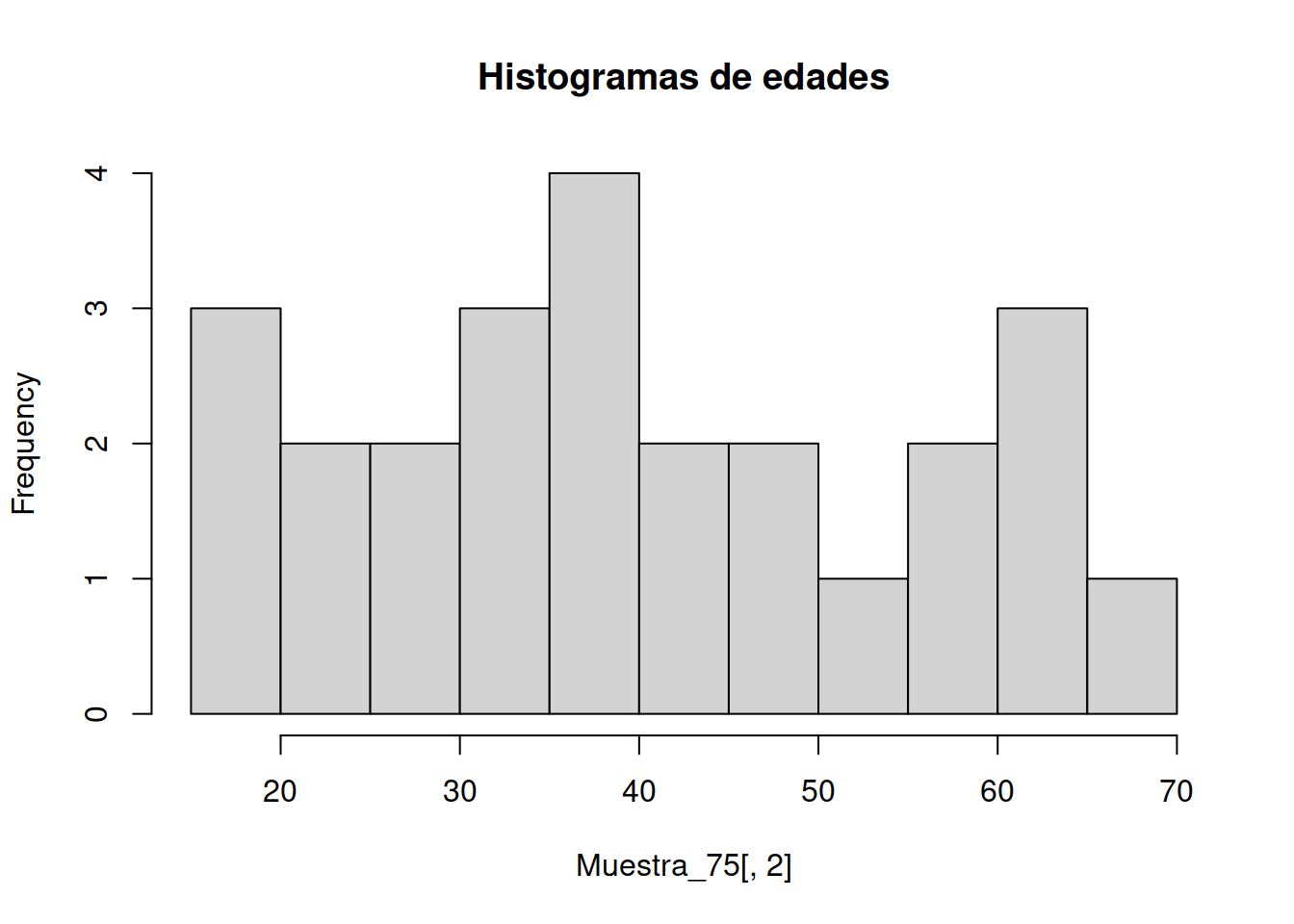
hist(Muestra_75[ ,2], # histogram
breaks = 3,
col="peachpuff", # column color
border="black",
prob = TRUE, # show densities instead of frequencies
xlab = "Edad",
main = "Distribución Etarea de la Muestra")
lines(density(Muestra_75[ ,2]), # density plot
lwd = 2, # thickness of line
col = "chocolate3")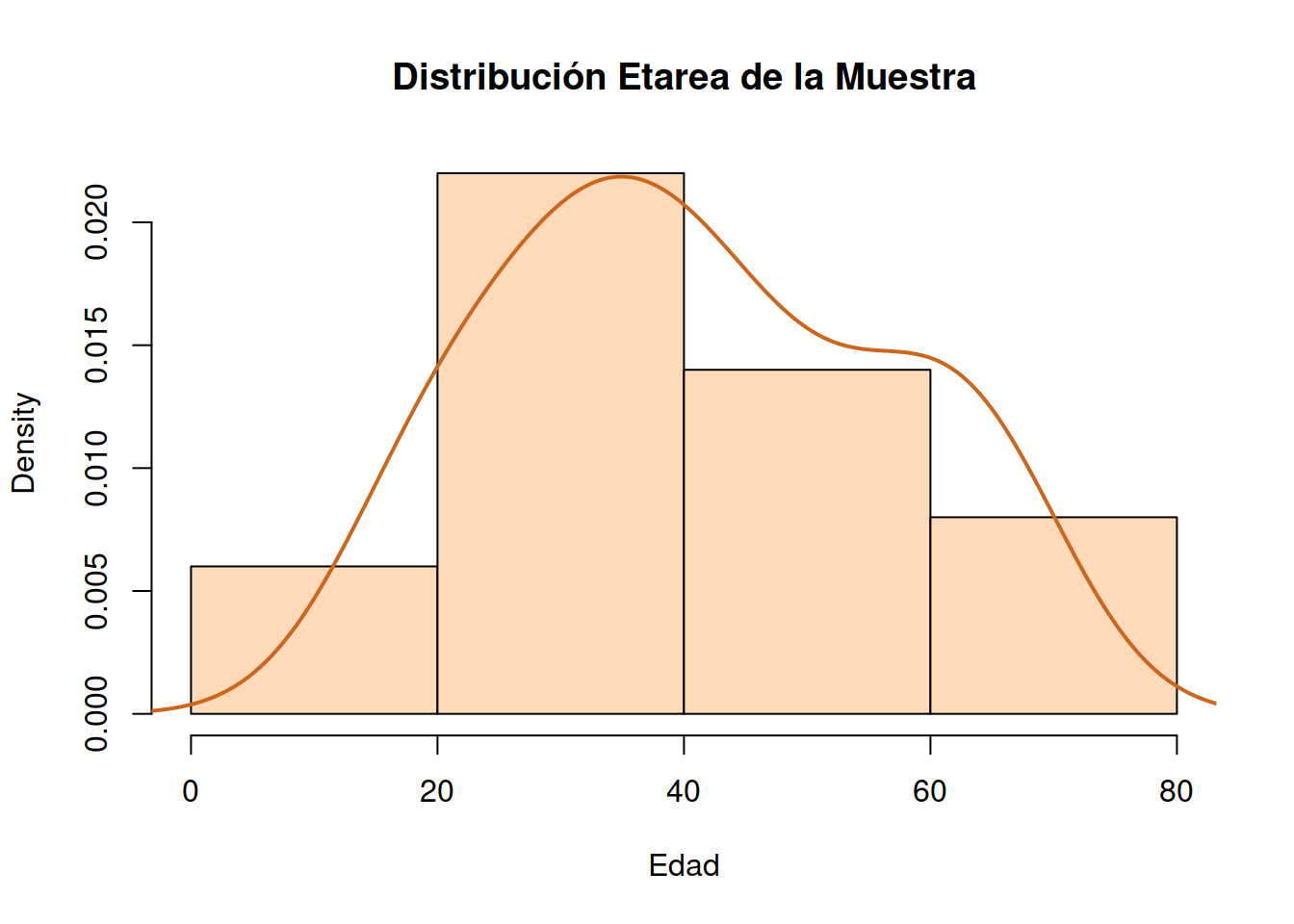
1.9 Varianza de Muestra y Población
La varianza de una población está expresada por la ecuación
\[\sigma^2 = \sum_{i=1}^{n} \frac {(x_i – \mu)^2} {N} \]
La varianza (de la muestrapuede ser calculada con el comando
var(Muestra_75[ ,2])Dato que la muestra siempre tiene un número considerablemente menor de individuos que la población la expresión que se usa para calcular la varianza de la muestra es distinta.
Varianza de la muestra es
\[ s^2 = \sum_{i=1}^{n} \frac {(x_i – \bar{x})^2} {n-1} \]
Puede encontrarse la varianza de la población sustituyendo los valores como se indica a continuación:
var_muestra <- var(Muestra_75 [ ,2])
var_muestra## [1] 244.61n <- length(Muestra_75[ ,2])
n## [1] 25n_over_n_1 <- n/(n-1)
n_over_n_1## [1] 1.041667Con esto valores podemos calcular la varianza de la población con la siguiente codificación
\[ \sigma = \frac {S} {\frac{n}{n-1}} \]
var_poblacion <- var(Muestra_75[ ,2]) / n_over_n_1
var_poblacion## [1] 234.8256El desvio estandar de la meustra es
dsm <- sd({Muestra_75[ ,2]})
dsm## [1] 15.64001En tanto que el desvió estándar de la población es
dsp <- sqrt(var_poblacion)
dsp## [1] 15.32402Un valor que es interesante calcular para comparar con la muestra del año 2018 es el desvío potential calculado como $ dsp_{%}= $
dspp_75 <- dsp/n
dspp_75## [1] 0.61296081.10 Repetir en análisis para la muestra 2018
Tarea !
Siempre comenzaremos nuestro trabajo con un análisis exploratorio básico, tal como hemos señalado. En este caso no hemos descartado ningún individuo de la muestra, pero sería conveniente hacerlo. El comando boxplot() te permitirá hacer una inspección rápida. Adisionalmente prueba el comando summary() para analizar la distribución de cunatiles y datos faltantes.
1.11 Construcción de un modelo
Nota!
En esta parte comenzaremos a desarrollar un modelo.
Utilizaremos una hipótesis simple. El modelo de regresión lineal podría ayudarnos a predecir para esta población a que edad deberíamos comenzar el diagnóstico de antígeno prostático. También realizaremos una comprobación basada en el modelo para saber si ha habido cambios significativos en los síntomas atribuibles al uso del herbicida
1.12 Hipótesis o pregunta de investigación
El proceso de investigación científica repetible parte de este tipo de premisa. Es un proceso iterativo de aproximación y revelación. Comenzaremos con una pregunta de investigación. ¿Será posible utilizar un modelo de regresión lineal para entender el comportamiento de estos datos?. Esta pregunta con el tiempo podrá ser formulada como una afirmación. Este proceso debe tener una investigación preliminar. De esteo modo podríamos expresar algo como El modelo de regresión lineal, que es muy utilizado en inteligencia artificial podrá darme respuestas a dos preguntas clave de este problema
1- El modelo regresión lineal puede predecir la probabilidad de aparición tiemprana de cancer. 2- Es posible utilizar el modelo construido para comparar dos poblaciones.
1.13 Bases de un modelo IA de regresión lienal
Para trabajar en este sentido R-Cran tiene posibilidades de desarrollar modelos de regresión lineal en un sólo comando. A pesar de ello construiremos un modelo desde CERO para entender como se procede en Inteligencia Artificial.
Todo modelo de regresión se basa en hallar los parámetros \(a\) y \(b\) de una ecuación de una recta.
\[ y = a*x + b \]
Donde: y es un número que varía entre 1 y 0
1 señala que se trata de un caso probable positivo, en tanto que
0 señala que es poco probable la aparición de cancer.
Para poder hallar los valores de estas variable o parámetros del modelo deberíamos utilizar los datos. En realidad con solamente dos datos de la muestra podríamos encontrar una recta que pase por estos dos puntos. Lo más aconsejable es no utilizar sólo dos, sino todos los puntos. Esto implica plantear un problema de dos ecuaciones con dos incógnitas y en rigor el método de los mínimos cuadrados sería lo más indicado.
Siguiendo con la idea de la construcción artesanal del modelo podemos decir que encontrando un punto significativo del modelo por el que pase la recta podremos agregar alguna estrategia para hallar la pendiente y con esos datos calcular \(a\) y \(b\).
1.14 Puntos significativos de modelo
Un punto significativo podría ser la moda de las edades y la moda de la variable categórica [1,0]. Se puede demostrar que en el modelo de regresión de los mínimos cuadrados este punto es el promedio de \(\overline{x}\) y el promedio de \(\overline{y}\). Pero existen otros valores verosímiles (Ver criterios de máxima verosimilitud de Ronald Fisher).
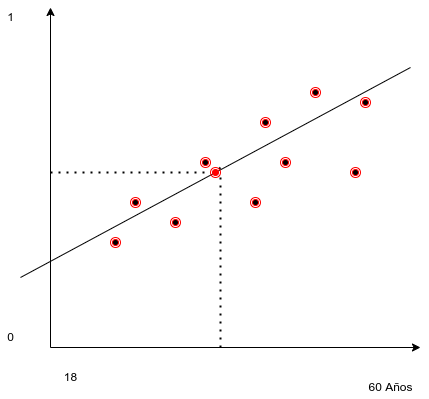
Modelos aproximado lineal
1.14.1 Cácluo de x e y significativos
Valor de y verosimil
index_ymax <- which.max(Muestra_75[ ,3])
ymax <- Muestra_75[index_ymax,3]
index_ymin <- which.min(Muestra_75[ ,3])
ymin <- Muestra_75[index_ymin,3]
y_sig <- (ymax-ymin) /2
y_sig ## [1] 0.5Valor de x verosimil
index_xmax <- which.max(Muestra_75[ ,2])
xmax <- Muestra_75[index_xmax,2]
xmax## [1] 66index_xmin <- which.min(Muestra_75[ ,2])
xmin <- Muestra_75[index_xmin,2]
xmin## [1] 17x_sig <- (xmax-xmin)
x_sig ## [1] 49El punto de coordenadas [24.5 , 0.5] es un punto por el que debe pasar la recta que construiremos.
1.14.2 Cáclulo de la pendiente
em valor \(a\) representa la pendiente de la recta. De modo que con los \(\Delta{x}\) y \(\Delta{y}\) podremos calcularlo facilmente
a <- ((ymax-ymin)/(xmax-xmin))
a## [1] 0.02040816\(a\) = valor de la pendiente es 0.02040816
Pendiente en grados
atan(a)## [1] 0.020405331.14.3 Cáclulo de la ordenada al origen.
Para calcular la ordenada al origen basta con poner \(x=\overline{x}\) del punto significativo que hemos adoptado en la formula de la recta usando el \(a\) calculado y despejar \(b\)
\[ y = a *x +b\] \[ b = y-a*x\] Cáclulo de b
y_sig## [1] 0.5x_sig## [1] 49a## [1] 0.02040816b <- y_sig-(a*x_sig)
b## [1] -0.51.15 Modelo de regresión lineal generalizado
En realidad este trabajo que hemos hecho puede ser realizado con solamente un comando en R-Cran.
Construiremos el dataset
x_muestra_75 <- Muestra_75[ ,2]
y_muestra_75 <- Muestra_75[ ,3]
mrlg <- as.data.frame( cbind(x_muestra_75,y_muestra_75))Construcción del modelo lineal
mi_formula <- y_muestra_75 ~ x_muestra_75
modelo_2 <- lm (mi_formula, data=mrlg)
modelo_2##
## Call:
## lm(formula = mi_formula, data = mrlg)
##
## Coefficients:
## (Intercept) x_muestra_75
## -0.61021 0.02178modelo_2$coefficients[2]## x_muestra_75
## 0.02177616modelo_2$coefficients[1]## (Intercept)
## -0.6102094Como vemos nos dice que la ordenada al origen es -0.610 y la pendiente es 0.021 muy parecidas a los valores \(a\) y \(b\) que obtuvimos antes.
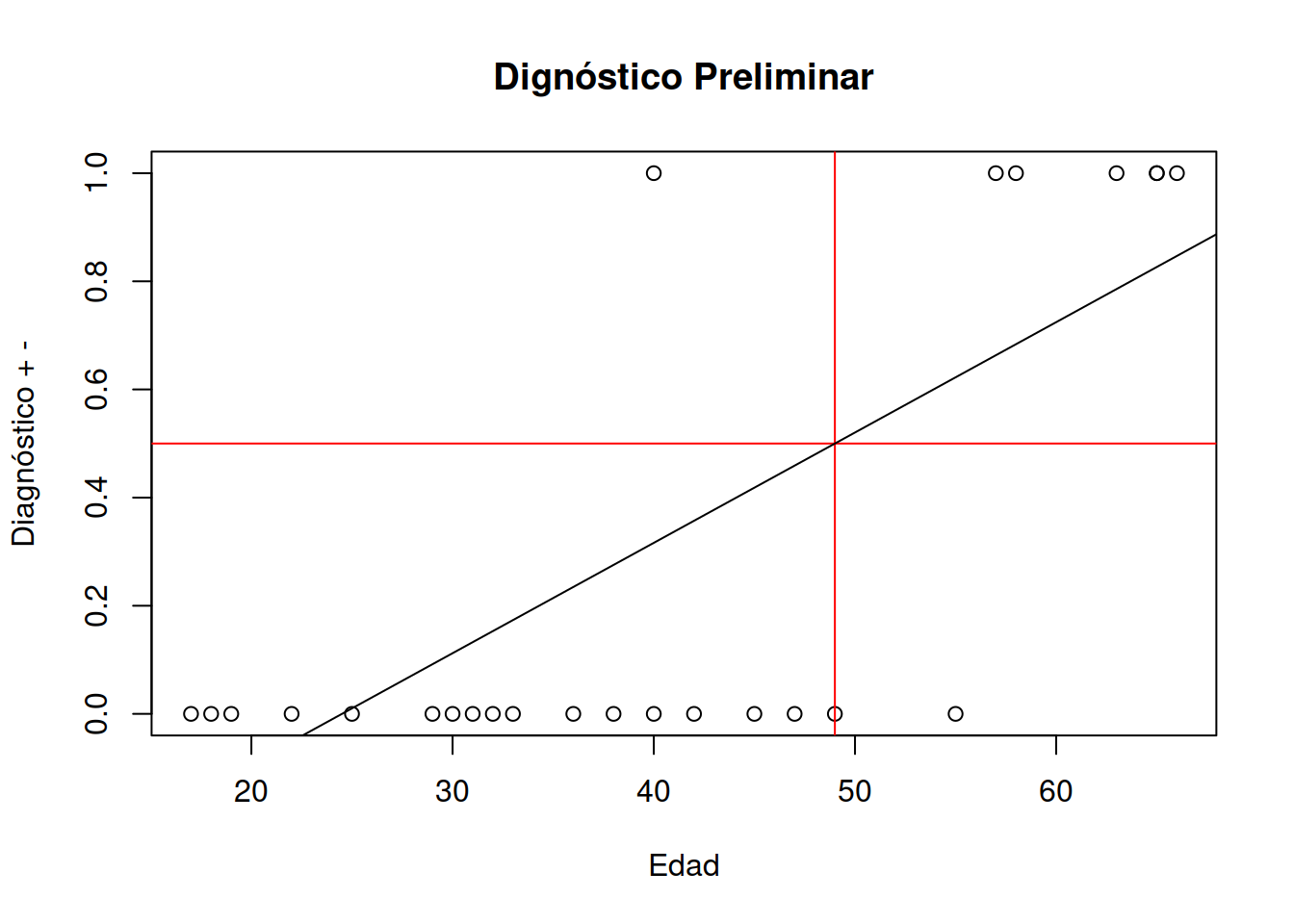
plot(mrlg)
abline(modelo_2,col="blue")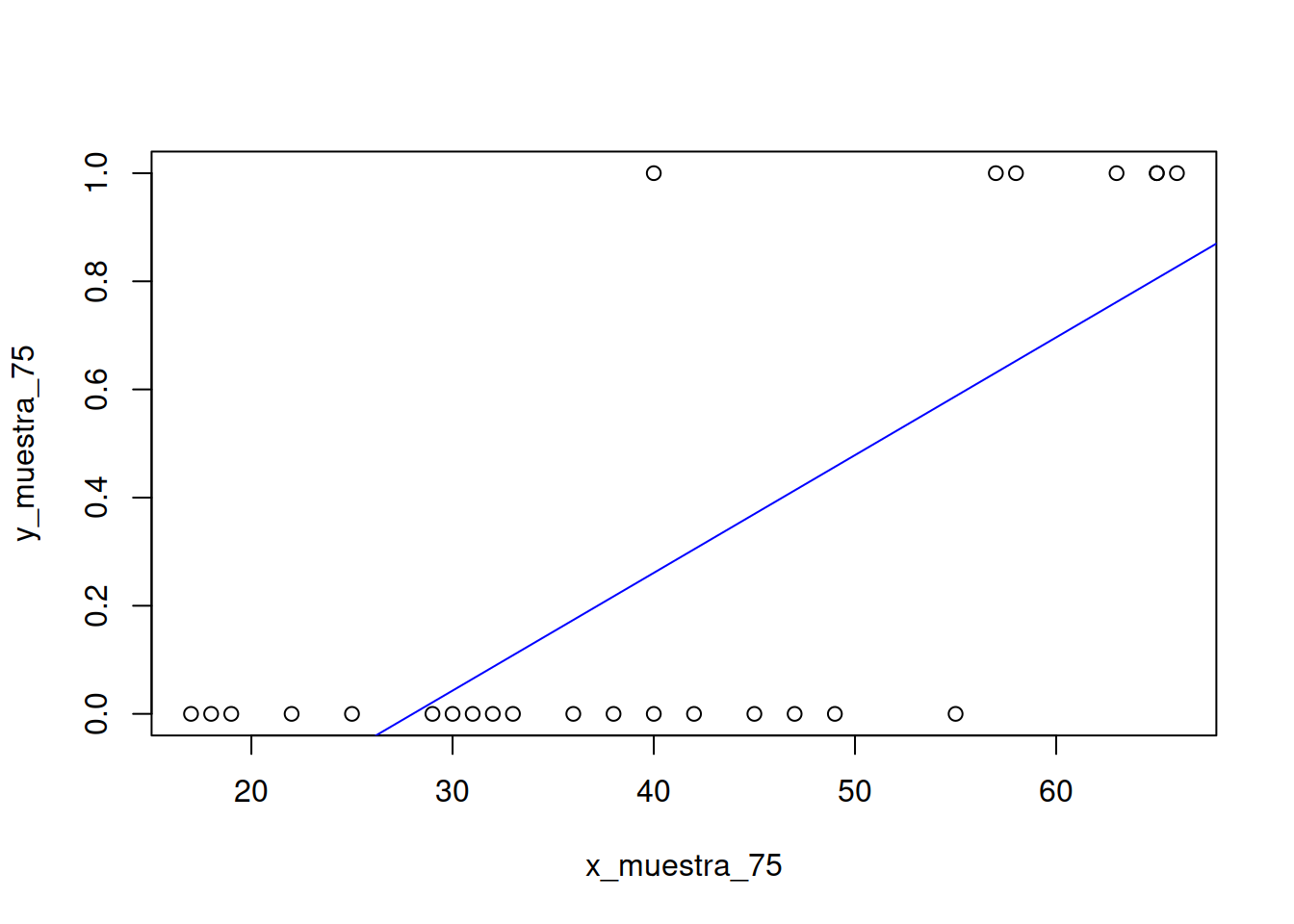
1.16 Modelo de regresión logística
Una de las cosas destacables del uso de IA es que puedo recurrir a muchos modelos para interpretar o predecir el comportamiento de los datos. Puedo generar (entrenar) el modelo o modelos y utilizar algún mecanismo de medición de la calidad de cada modelo y en base a ello utilizar IA para seleccionar el que más se adapta a mis datos.
Hay una distribución de probabilidades llamada Distribución Logística que puede utilizarse (del mismo modo que la distribución lineal se usa para el modelo de regresión lineal generalizado) para armar una regresión lineal logística.
La forma típica de la distribución logística normalizada tiene la siguiente ecuación paramétrica y luce como se ve en el ejemplo.
\[ \sigma(x)= \frac{e^x}{(e^x+1)} = \frac{1}{1+e^{-x}}\]
curve((1/(1+exp(-x))),-10,10,col ="red")
abline(0.5,0.05,col="green")
text(-8,0.2,"Rergresion Lineal",col="green")
text(6,0.8,"Rergresion Logística",col="red")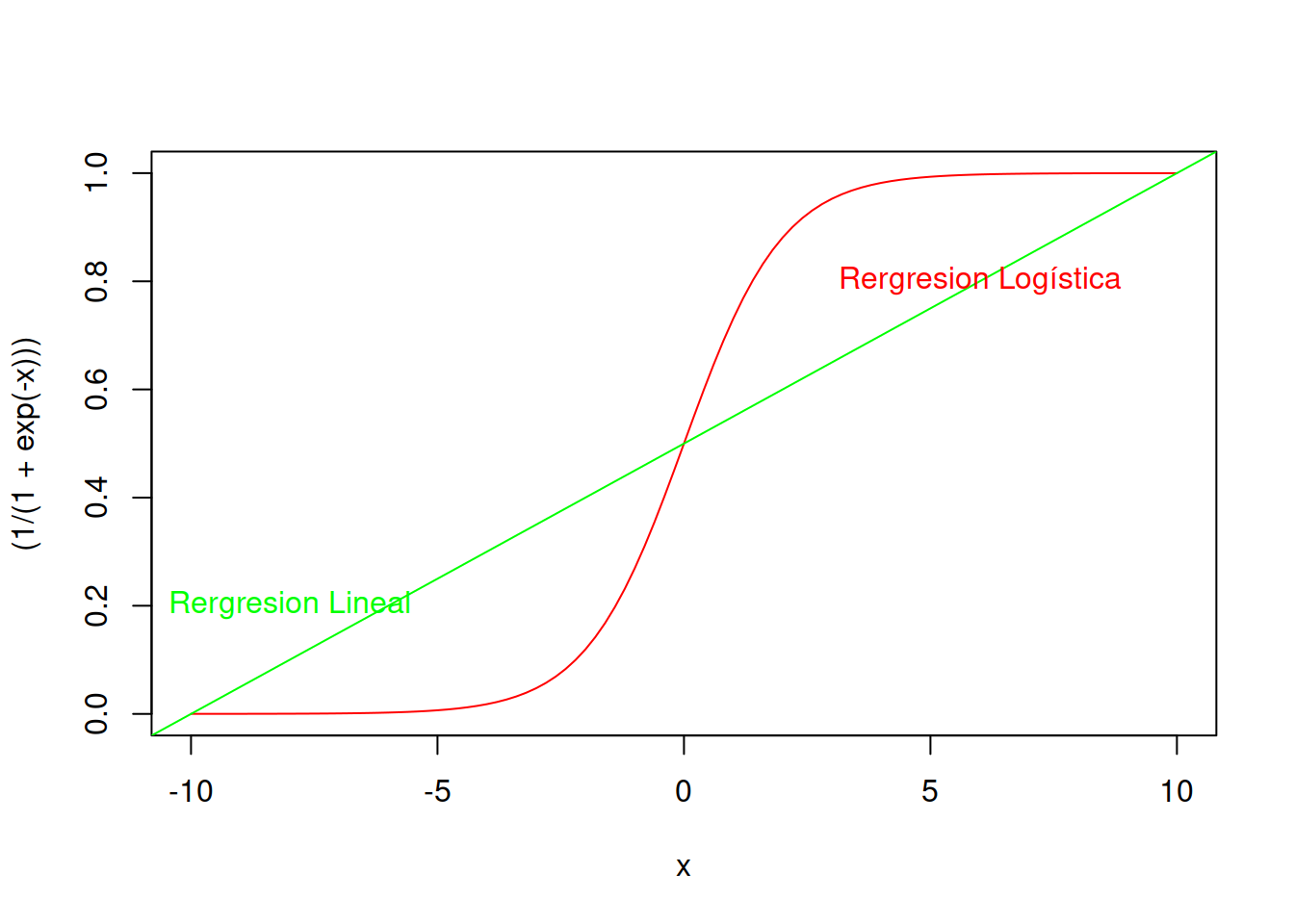
Como pude verse el modelo de regresión logística es mas sensible a los datos y proporcional resultados más verosímiles, pero aún mantienen error admisible. De todos modos esta análisis visual nos indica que ya tenemos una alternativa que es mejor que nuestro modelo lineal inicial.
La función de distribución de probabilidad acumulada de la regresión logística es:
\[g(F(x))= ln \left[ \frac{F(x)}{1-F(x)} \right] = \beta^0 + \beta_1*x \] Al igual que en la regresión lineal es posible (aplicando logaritmos) encontrar los parámetros \(\beta_0\) y \(\beta_1\) con solamente cuatro datos en la muestra. El error será inadmisible, pero es algo parecido a armar una regresión lineal con sólo dos muestras.