6 Redes Neuronales y Clusters
6.1 Implementación NeuralNet
6.1.1 Caso de estudio sistema de emergencias medicas
Este trabajo ha sido realizado en el año 2018 por alumnos del MBA de Ciencias Económicas de la UNCuyo.
- Cahiza Victoriano
- Danitz Santiago
- Drago Graciela
- Hernandez Paula
- Orduña Victoria
- Pocognoni Luciana
- Pagliano Diego
Se puede encontrar una copia del trabajo en el sitio de web https://support.rstudio.com/hc/en-us/sections/200130218-R-Presentations
6.2 Contexto General
En términos generales se suele encuadrar la enseñanza de la técnica redes nueronales como paso posterior al modelo de regresión lineal. En analítica de datos este segundo paso no difiere mucho de una predicción. De hecho para comparar la performance realizaremos una comparación entre ambas predicciones.
En general la biblioteca Neural Net de Python y R-Cran tiene la característica de ser menos exactas que regresion lineal. Tienen más sensibilidad a los datos, pero en cambio tienen una velocidad de procesamiento para la predicción pasmosamente alta.
En este caos imaginen una situación de una comuna de latinoamética y caribe que es polulosa, tiene pocas ambulancias y resiliencia hospitalaria y debe enfrentar una pandemia. Imagine el caso de estar en una instancia previa al triage. Asignar las ambulacias o vehiculos adaptados, así como predecir la demora con la que llegarán al paciente es una actividad típica de decisión de la administración de operaciones, en la que los postulados de la logística priman, pero están sujeto a la limitación de costos y recursos.
El siguiente trabajo es un ejercicio donde se busca experimentar con herramientas de simulación y predicción como ser NeuralNet y Regresión Lineal mediante el uso del software RStudio.
6.3 Introducción
En primer lugar se busco una base amplia con importante cantidad de datos de la cual se pudiera inferir resultados útiles.
Se logro obtener la base del servicio coordinado de emergencias, en formato .csv, con la cual desarrollamos nuestro trabajo.
Luego realizamos dos simulaciones una utilizando la base con todas las columnas originales (19) y otra filtrando las columnas sin aportes no significativos (10) según los coeficientes t de Student.
Este mismo análisis prodíamos haberlo conseguido eliminando las columnas que la matriz de covarianza nos señala que no tienen independencia estadística.
6.4 Desarrollo
Para trabajar la base de datos en la plataforma R, primero debemos importarla:
library(readxl)
BD <- read_excel("emergencias MBAE 2016.xlsx")Es fundamental asegurarnos que no existan celdas vacías: Las celadas NA o na (not available) son las instancias que R-Cran ha hallado vacías (sin ceros o son textos) Sumaremos todos los registros de cada columna que tienen na's
apply(BD,2,function(x) sum(is.na(x)))## color motivollamado
## 0 0
## movil base
## 0 0
## horadespachomovil horasalidabase
## 0 0
## horallegadadomicilio edad
## 0 0
## sexo zona
## 0 0
## colormedico
## 0Para poder entrenar la red neuronal, y luego validarla debemos dividir aleatoriamente los datos
Uno de los sets lo utilizaremos para hacer aprendizaje no supervisado. Es decir para entrenar la red neuronal sin supervisión. En tanto el set complementario podremos usarlo para ver si al tratar de predecir el resultado de una columna que nos interesa explicar, la red neuronal alimentada con el resto de los datos de esa fila nos da el mismo resultado.
La sunción sample toma un conjunto de datos aleatorios de la variable que hemos llamado DB. Si el primer parámetro es 1, le indicamos que queremos muestreo de datos numéricos. Ver la ayuda de asmple para más datos. Le señalamos la cantidad de datos (total de datos de DB) y la muestra (75% de DB) la mariable índice solamente tiene el número de registro del renglón soleccionado. Crearemos un vecto llamado test que tiene la misma estructura que DB pero solamente el 75% de sus instancias.
indice <- sample(1:nrow(BD),round(0.75*nrow(BD)))
train <- BD[indice,]
test <- BD[-indice,]6.5 Generalizacion para la regresión lineal
Previo a trabajar con RN, realizamos el modelo de regresión lineal, que usaremos de comparación. En este caso la variable dependiente que hemos elegido es el campo “horallegadadomicilio”
lm.fit <- glm(horallegadadomicilio~., data = train)En este caso el comando generalized linear model intentará explicar la hora de llagada en función de todas las otras columnas, esto se señala con el punto después del circunflejo.
6.5.1 Calidad del modelo lineal
summary(lm.fit) alt text(summaryglm.png)En base al modelo lineal que determinamos, realizamos una predicción en funcion del conjunto de datos de prueba y se evalúa el error medio cuadrático:
6.5.2 Primera predicción
Calcularemos el error medio cuadrático MSE del modelo.
pr.lm <- predict(lm.fit,test)
MSE.lm <- sum((pr.lm - test$horallegadadomicilio)^2)/nrow(test)
MSE.lm## [1] 5.480552e-05Este valor se corresponde con un error de 6 segundos en promedio. Note la exactitud de la predicción sobre el set de prueba.
Para lograr resultados lógicos y que la red aprenda mejor, debemos realizar un preprocesamiento de datos con que entrenaremos a la red neuronal.
Esto tienen por objetivo solucionar tres problemas.
Primero reducri el error de punto flotante. Este error lo comenten todos los procesadores cuanto tienen que realizar muchas operaciones en las que se suman números grandos (como los acumulados) con incrementales que son muy pequeños.
Utilizar técnicas de normalización, que siempre la ciencia estadistica nos recomienda
Maximizar la entropia de los datos escalados que acorta el camino numérico a la solución.
maxs <- apply(BD, 2, max)
mins <- apply(BD, 2, min)
scaled <- as.data.frame(scale(BD, center = mins, scale = maxs - mins))
train_ <- scaled[indice,]
test_ <- scaled[-indice,]la función apply tiene tres parámetros
DB el set de datos sobre el que aplicaremos el comando
El segundo comando puede ser 1 (eso refiere a que nos interesan las filas), o 2 (que hace referencia a las columnas).
Tercer parmametro pueden ser comandos como máximo, mínimo, como (parecido), etc.
En este caso tenemos los valores máximos y minimos de cada columan.
Finalmente escalamos los vectores y lo transformamos en un data frame para tenerlo accesible más rápido en la memoria RAM.
Notar que los vectores train y test son complemento a uno (ver el signo menos en índice)
6.6 Construcción de la Red Neuronal
A continuación en esta segunda parte construimos la red neuronal, con una capa de entrada de 10 neuronas, dos capas ocultas de 6 y 3 cantidad de neuronas, y una capa de salida de una neurona.
Esta neurona final nos dará la predicción de la hora de llagada.
6.6.1 Grpafico de la Red Nuronal
library(neuralnet)
n <- names(train_)
f <- as.formula(paste("horallegadadomicilio ~", paste(n[!n %in% "horallegadadomicilio"], collapse = " + ")))
nn <- neuralnet(f,data=train_,hidden=c(6,3),linear.output=T)plot(nn, rep = "best")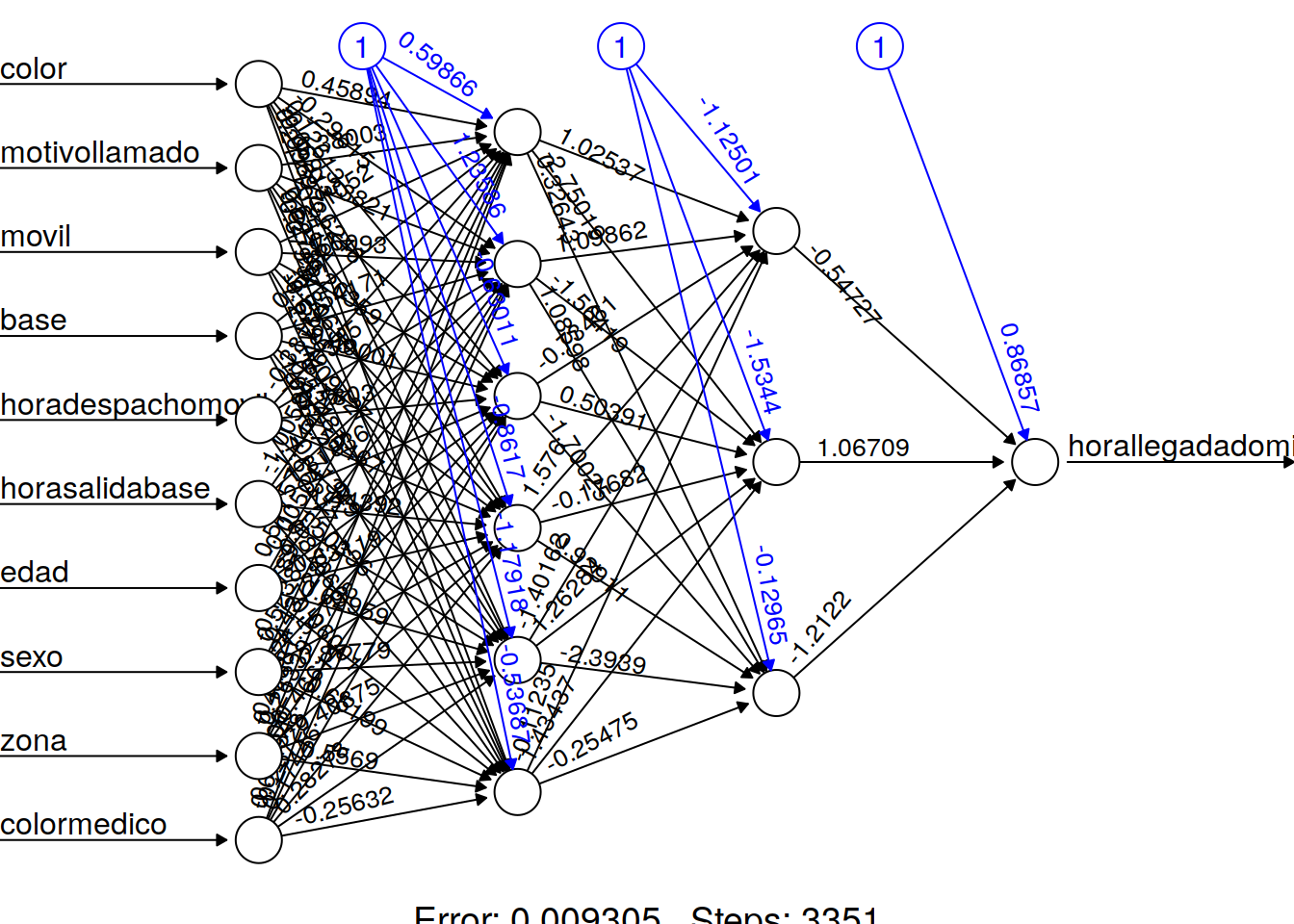
Los valores azules son el sesgo (bais) que puede tomarse como una suerte de ordenada al origen Los valores negros son los pesos y en realidad esto permitria asimilar a la red a un conjunto de pequeños modelos lineales que sumados constituyen la red.
Representación gráfica de la red con los pesos en cada conexión. Las lineas negras muestran las conexiones entre cada capa y los pesos en cada conexión, mientras que las lineas azules muestran el termino de sesgo agregado en cada paso.
En base a esta red neuronal, procedemos a predecir el horario de llegada, en funcion del conjunto de datos de prueba,y por ultimo calculamos el error medio cuadrático
pr.nn <- compute(nn,test_[,1:10])
pr.nn_ <- pr.nn$net.result*(max(BD$horallegadadomicilio)-min(BD$horallegadadomicilio))+min(BD$horallegadadomicilio)
test.r <- (test_$horallegadadomicilio)*(max(BD$horallegadadomicilio)-min(BD$horallegadadomicilio))+min(BD$horallegadadomicilio)
MSE.nn <-sum((test.r - pr.nn_)^2)/nrow(test_)Ahora podemos comparar los resultados de la predicción usando el modelo de regresión lineal y la red neuronal
print(paste(MSE.lm,MSE.nn))[BD completa] "0.0572576887890648000 4.1603006552126300"
[BD sin aportes no significativos] "0.0000799978154659859 0.0485608687457361"
Estos valores se interpretan como un error promedio de 1h 22min contra 4 días 3h 50min en el primer caso.
Y en el segundo caso 8 segundos contra 1h 9min.
Los mismos son aproximados ya que depende de la división de datos aleatoria realizada anteriormente.
6.7 Real vs Predicción
De forma gráfica las predicciones de ambos sistemas, son las siguientes:
plot(MSE.lm,MSE.nn)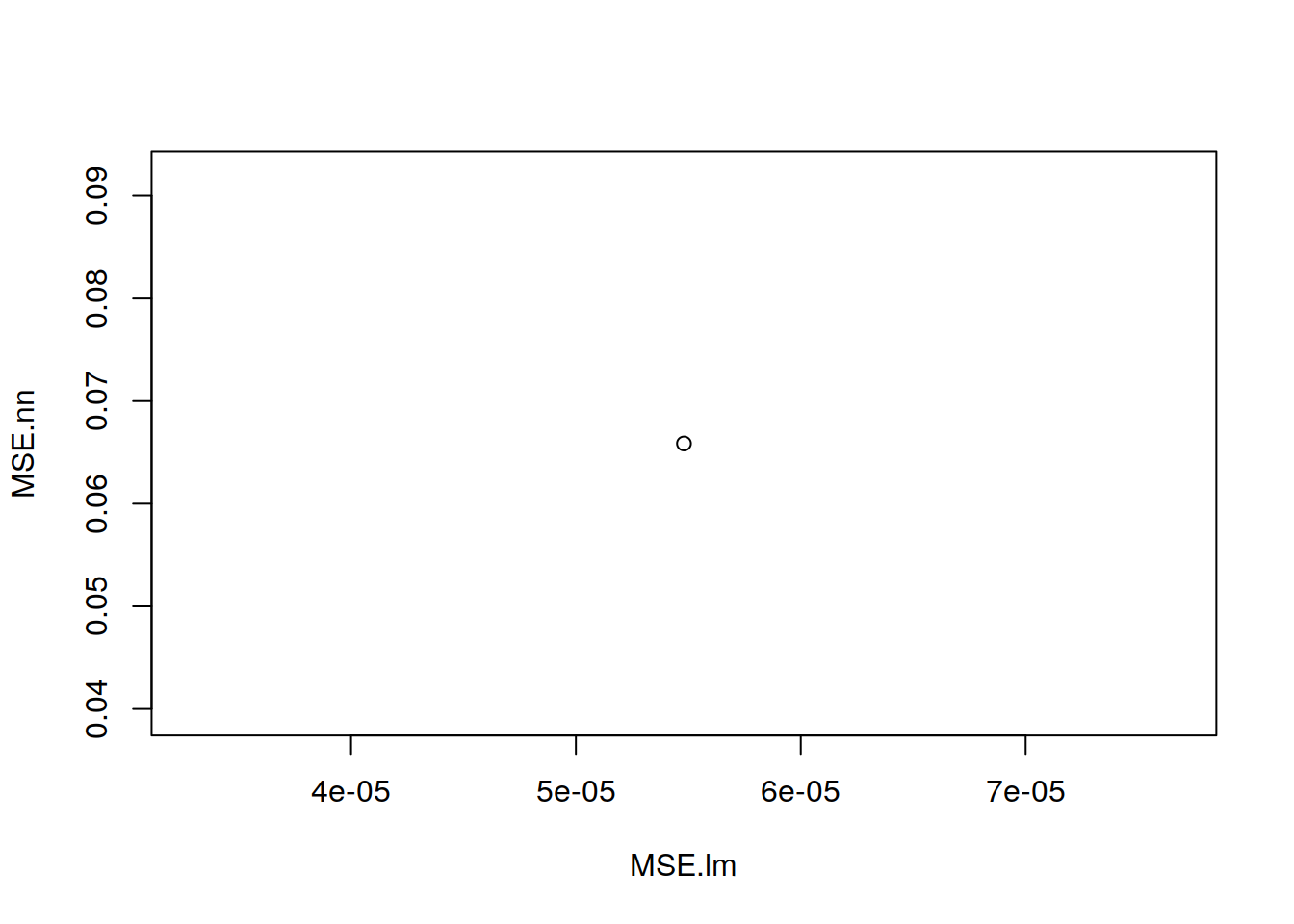
6.8 Validación cruzada
Validación cruzada, es un paso muy importante de la construcción de modelos predictivos.
A continuación realizamos una prueba de tren dividida, y comparamos los MSE de 10 redes neuronales construidas con 10 conjuntos distintos de datos obtenidos de forma aleatoria
library(boot);set.seed(200);lm.fit <- glm(horallegadadomicilio~.,data=BD); cv.glm(BD,lm.fit,K=10)$delta[1]##
## Attaching package: 'boot'## The following object is masked from 'package:psych':
##
## logit## [1] 9.649756e-05set.seed(450); cv.error <- NULL; k <- 10; for(i in 1:k){iindice <- sample(1:nrow(BD),round(0.9*nrow(BD))); train.cv <- scaled[iindice,];test.cv <- scaled[-iindice,]; nn <-neuralnet(f,data=train.cv,hidden=c(6,3),linear.output=T); pr.nn <-compute(nn,test.cv[,1:10]); pr.nn <-pr.nn$net.result*(max(BD$horallegadadomicilio)-min(BD$horallegadadomicilio))+min(BD$horallegadadomicilio); test.cv.r <-(test.cv$horallegadadomicilio)*(max(BD$horallegadadomicilio)-min(BD$horallegadadomicilio))+min(BD$horallegadadomicilio); cv.error[i] <- sum((test.cv.r - pr.nn)^2)/nrow(test.cv)}6.9 Resultado
mean(cv.error)## [1] 0.1203585cv.error## [1] 0.03518276 0.14207185 0.02988265 0.11519926
## [5] 0.04842905 0.03456001 0.05028228 0.31465322
## [9] 0.27701975 0.15630367boxplot(cv.error)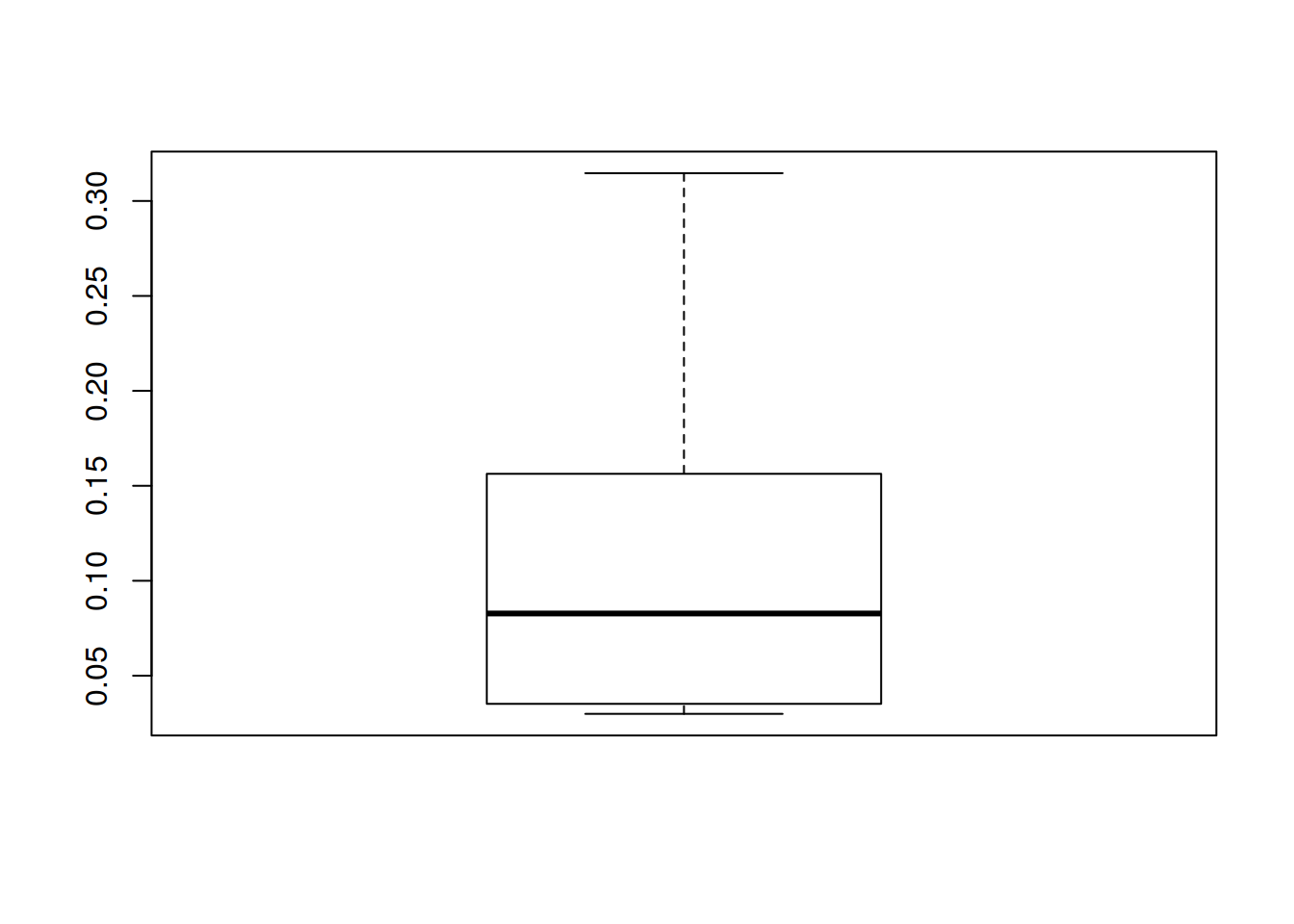
Para interpretar gráficamente los resultados de la validación utilizamos un diagrama de caja.
alt text (comparacionBox.png)Se observa una mediana de 2.33 con un mínimo de 0.51 y un máximo de 14.08. Como valor atípico tenemos 22.50.
Contra una mediana de 0.83 con un mínimo de 0.035 y un máximo de 0.31. Y sin valor atípico.
6.10 Conclusiones
Se observa que la regresión lineal ajusta mejor en ambos casos.
Al descartar las columnas que no no aportan datos significativos se obtiene un mejor ajuste.
Se estima que realizando otro método de preprocesamiento se obtendrán resultados distintos de la red neuronal.
6.11 Referencias
Entrenamiento de Redes Neuronales en R;neuralnet package (Ricardo Palma - Gustavo Masera)
https://support.rstudio.com/hc/en-us/sections/200130218-R-Presentations