11 Árboles Clasificadores y Toma de Decisión
Actividad del Jueves 29 de Octubre
Recuerda bajar los set de datos desde <https://themys.sid.uncu.edu.ar/rpalma/R-cran/Analitica_Industrial/>
11.1
11.2 Clasificación con Diagrama Aluvial
El diagrama aluvial es una variante de un gráfico de coordenadas paralelas (PCP) pero para diferencia de la versión tradicional se usan variables categóricas. Las variables se asignan a ejes verticales que son paralelos. Los valores se representan con bloques en cada eje. Las observaciones se representan como aluviones (sing. "Aluvión") que abarcan todos los ejes de izquierda a derecha.
Crear diagramas aluviales es sencillo y para ello usamos la biblioteca aluvial con la función aluvial (). Este es un ejemplo que utiliza el conjunto de datos del sistema nacional de innovación de Argentina. Como todo buen resumen de datos no tiene series históricas, de modo que ARIMA no puede usarse. Vamos a convertir este colplejo de números en un marco de datos util para la toma de decisión.
APPncia <- read.csv2("agencia.csv")
tit <- as.data.frame(APPncia, stringsAsFactors = FALSE)
head(tit)## Organismo Sexo APP Exito Freq
## 1 Conicet Hombre PyME_ANR No 0
## 2 Inta_Inti Hombre PyME_ANR No 0
## 3 Universidad Hombre PyME_ANR No 35
## 4 Startup_EBT Hombre PyME_ANR No 0
## 5 Conicet Mujer PyME_ANR No 0
## 6 Inta_Inti Mujer PyME_ANR No 0
## Monto
## 1 5.045360
## 2 47.610275
## 3 5.644619
## 4 16.222262
## 5 33.161698
## 6 29.141628Esta variable tit (llamada así por que refleja la titularidad de las empresas financiadas) tiene las siguientes columnas:
names(tit)## [1] "Organismo" "Sexo" "APP"
## [4] "Exito" "Freq" "Monto"Organismo: Institución a en la que nace el proyecto
Sexo: Indica si quien presenta el proyecto es hombre o mujer
APP: Tipo de financiamiento Público Privado
Freq:Cantidad de empleos que generó
11.3 Detalle de las variables categóricas
En este caso no hemos podido conseguri un dataset bien muestrado, sino que por la necesidad de indagar la igualdad de géneros se nos ha suministrado una muestra sesgada, tal como señala el análisis de las variables categóricas.
summary(tit[ ,1:4])## Organismo Sexo APP
## Conicet :32 Hombre:64 C_Fiscal:64
## Inta_Inti :32 Mujer :64 PyME_ANR:64
## Startup_EBT:32
## Universidad:32
## Exito
## No :64
## Yes:64
##
## 11.4 Valores de Empleos Generados (Freq)
empleos <- sort(tit$Freq)
plot(density(empleos))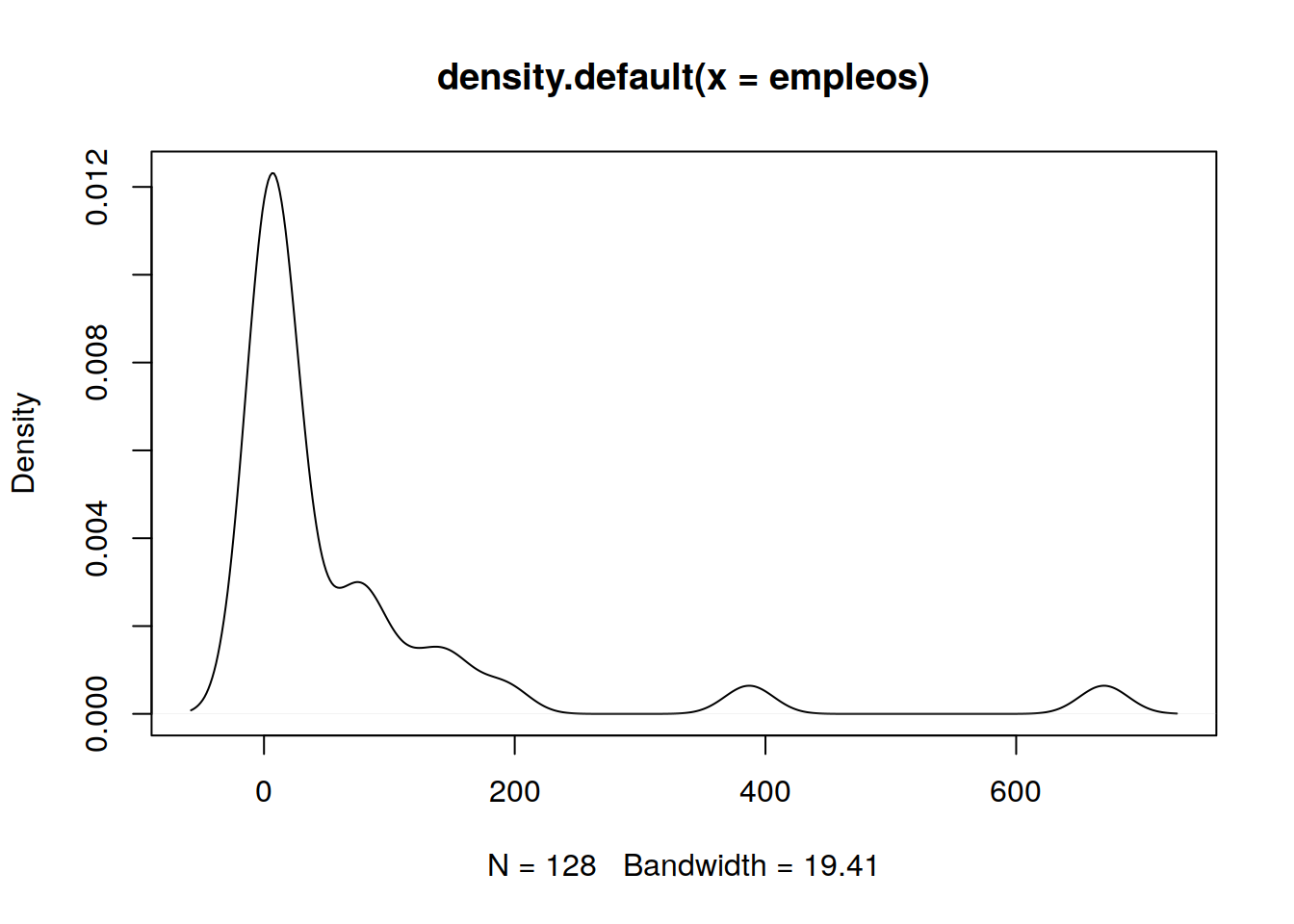
11.4.1 Enálisis del ploteo de Empleos
plot(empleos,main = "Puestos generados",xlab="Proyectos",type = "l" , col="blue")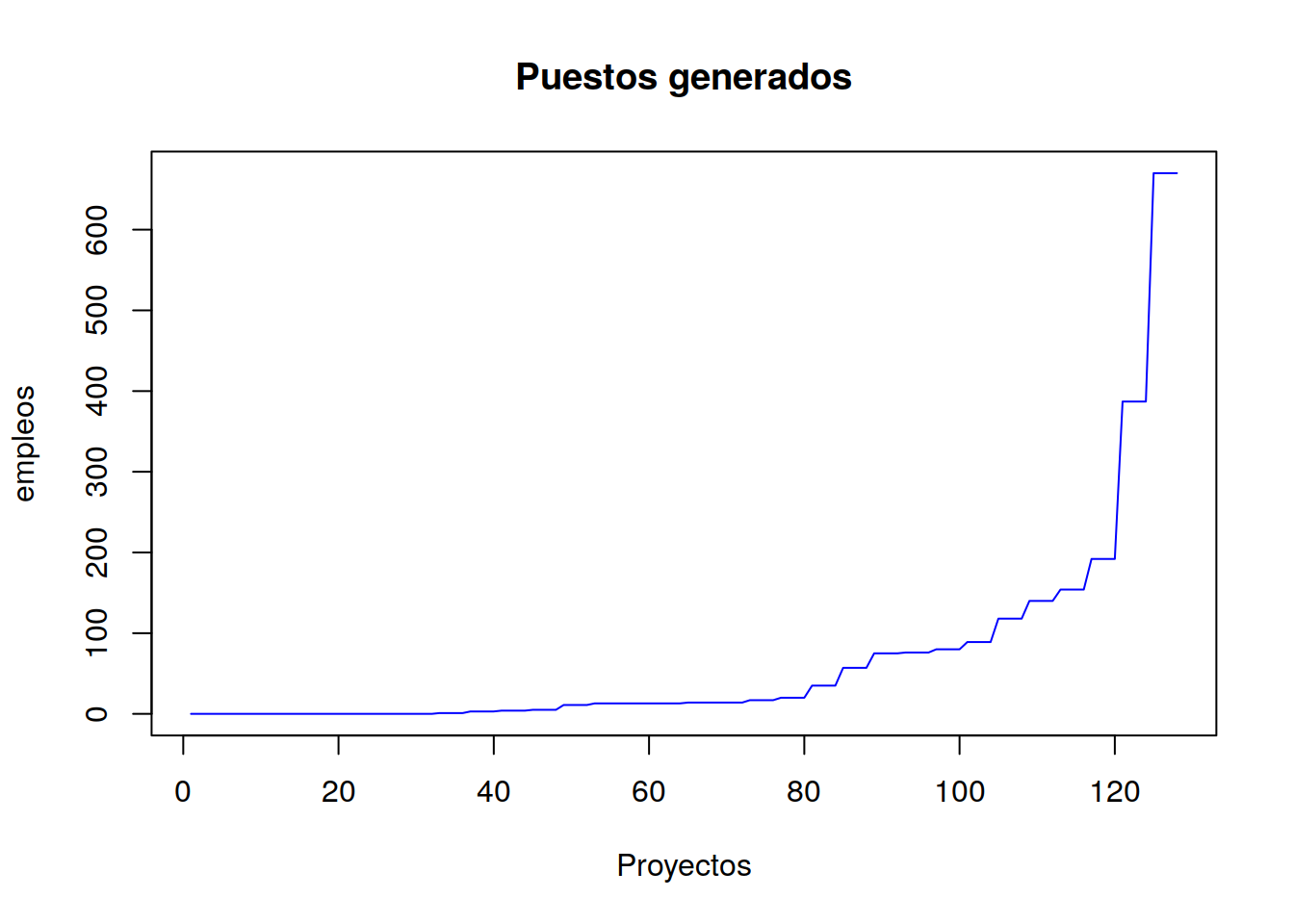
11.4.2 Histograma de Montos Financiados
En todos los casos los proyectos tienen un financiamiento de contraparte. El requisito para obtenerlo es demostrar que ya tienen mercado.
hist(tit$Monto, main ="Monto", xlab = "millones de pesos", ylab="proyectos")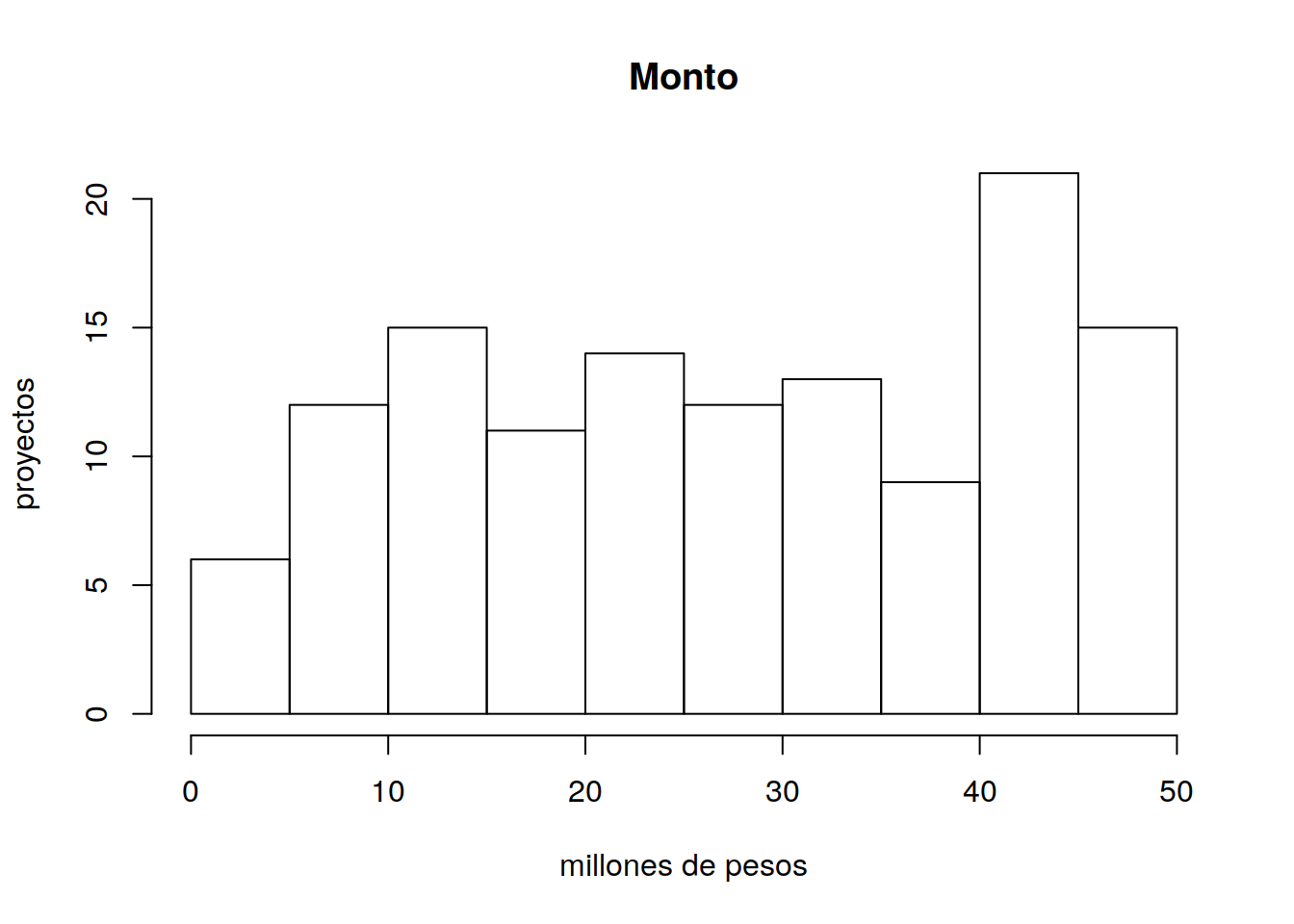
11.5 Montos Financiados
montos <- tit$Monto
# montos <- sort(montos)
plot(montos, type="s")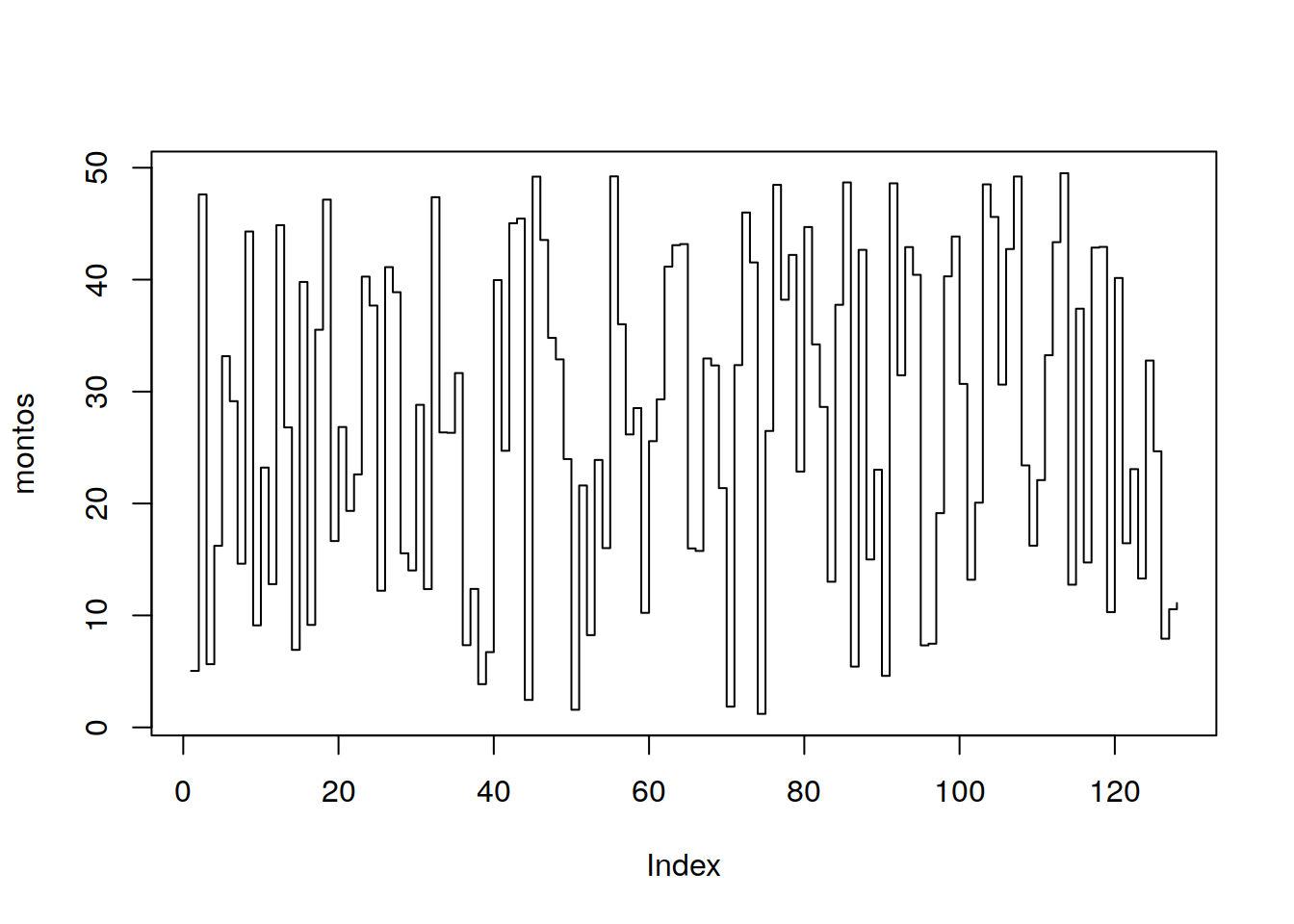
library(ggplot2)##
## Attaching package: 'ggplot2'## The following objects are masked from 'package:psych':
##
## %+%, alphaequis <- seq(1,length(montos))
MONTOS <- cbind(equis,montos)
colnames(MONTOS,c("equis","montos"))## [1] "equis" "montos"MONTOS <- as.data.frame(MONTOS)
p <- ggplot(MONTOS, aes(equis, montos))
p + geom_point() + geom_smooth()## `geom_smooth()` using method = 'loess' and formula 'y ~ x'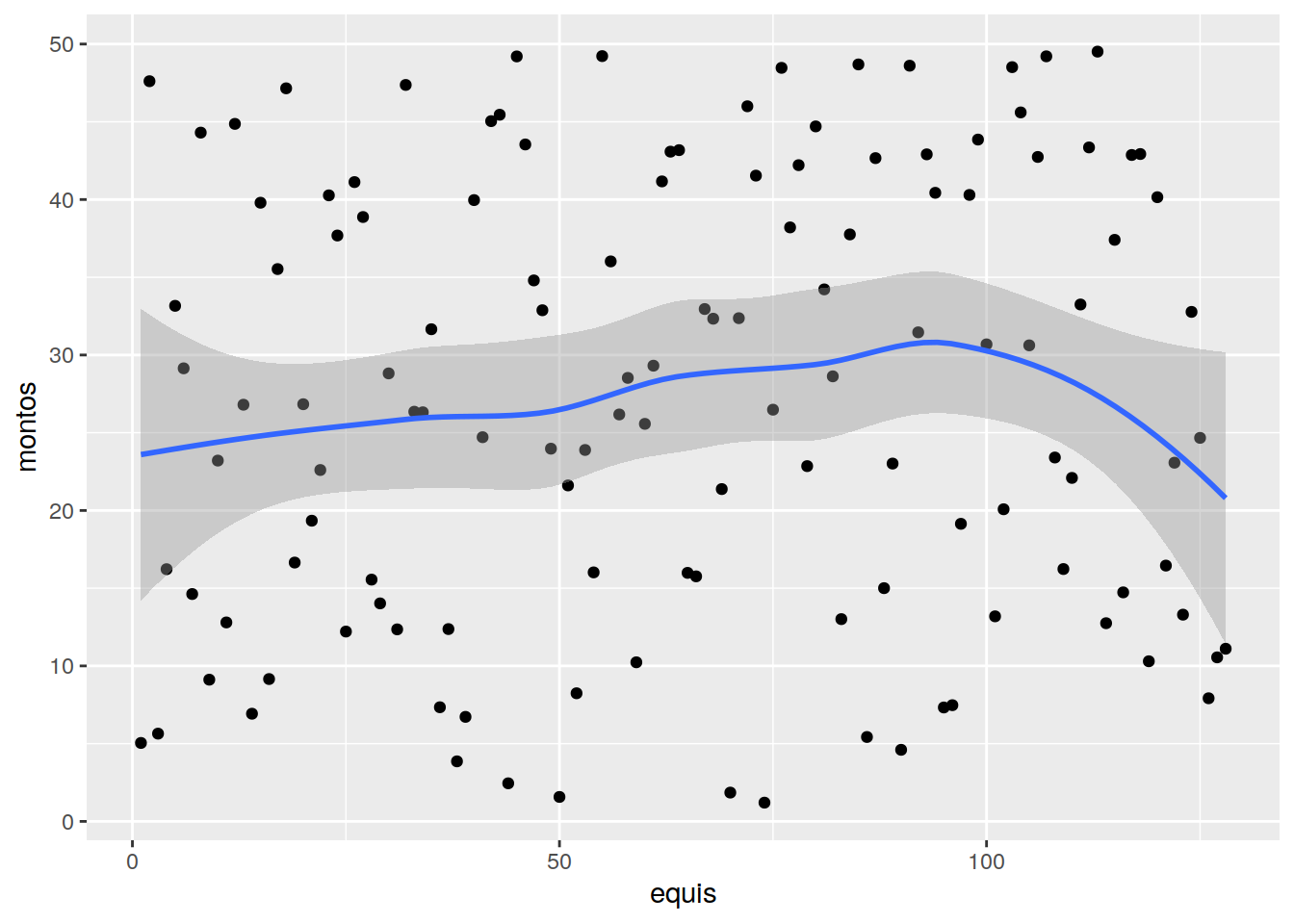
11.5.1 Creando el Diagrama
Procederemos a invocar la biblioteca alluvial (recuerda que primero debes cargarla por única vez con el comando install.packages)
Este es un ejemplo muy cargado de atributos, no mires del código los descriptores gráficos y de color de los objetos. El objetivo de aprendizaje pretende que "juegues con la estética hasta obtener los resultados que pongan en evidencia lo que descubras".
library(alluvial)
alluvial(tit[ ,1:4],freq = tit$Freq , col= ifelse(tit$Exito == "No", "Red","Green"), cex= 0.5)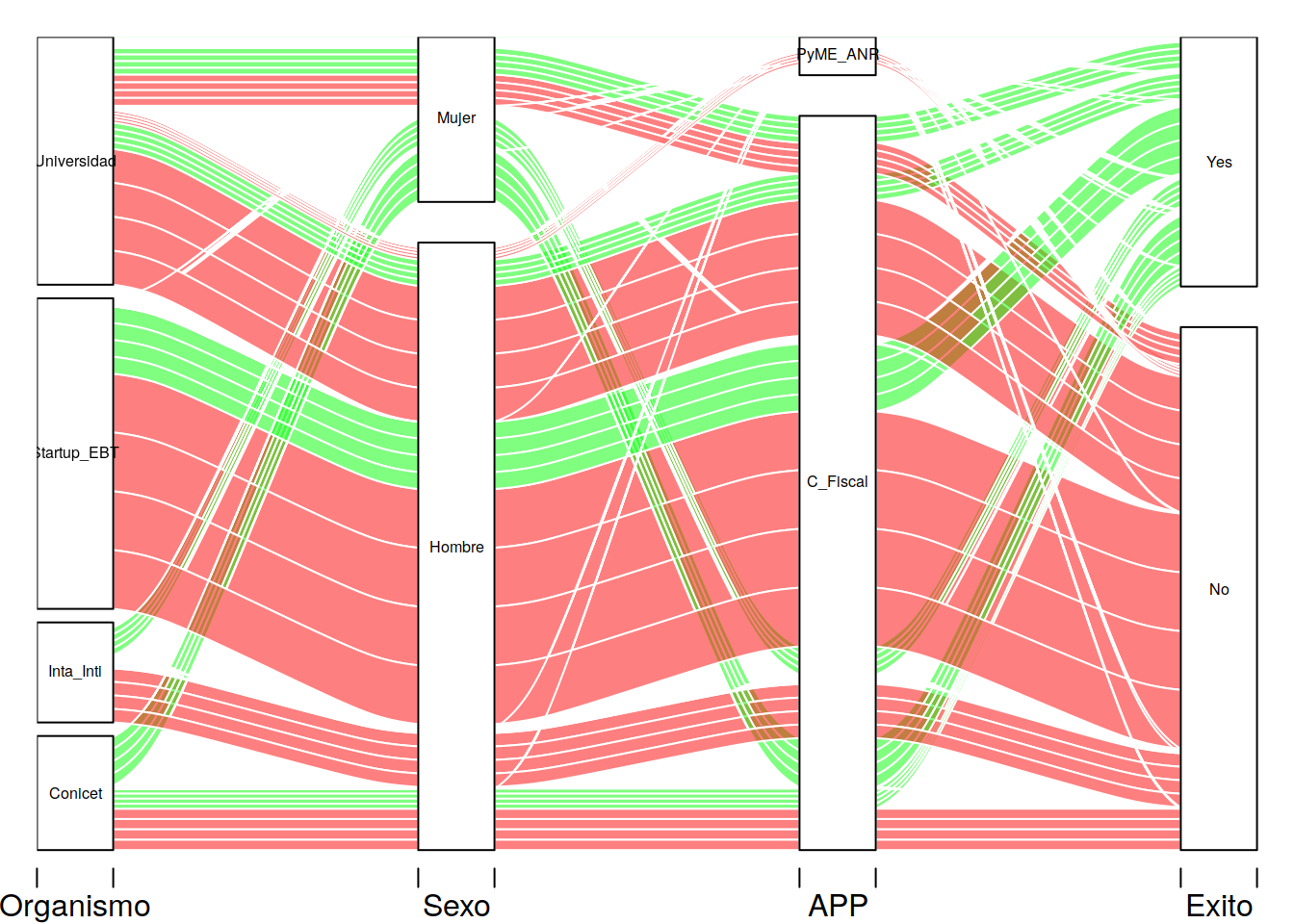
Explicaremos línea a línea que hace cada parámetro del comando alluvial
tit[ ,1:4]: Para operar alluvial necesita que le demos un dataframe de variables categóricas en este caso le asignamos las cuatro primeras columnas del dataset completo.
freq = tit$Freq Hemos denominado a la columna Freq con el mismo nombre del parámetro por que hemos comprobado que este el el argumento que más confusión genera. En este caso Freq representa la cantidad de puestos de trabajo que generó el proyecto. En muchos casos el proyecto fue un fracaso y no pudieron devolver en dos años el monto que se les financiaba, pero con la formación de los recuros humanos y en algunos casos con equipos que fueron liquidados como indemnizaciones a los empleados o socios que aportaron capital de contraparte, esto generó empleo.
col= ifelse(tit$Exito == "No", "Red","Green") col indica como siempre el color. En este caso le digo con el comando ifelse que si la columna Exito es No use color Rojo, en otros casos use color Verde.
cex= 0.5 Es un factor de multiplicación de la escala de texto.
11.5.2 Algunos ejemplos de aluvial
Ya hemos armado el dataframe y acomodado los datos para que puedan ser impresos veremos el más simple de los diagramas que podemos hacer. Por defecto alluvial nos imprme los graficos en color gris y usa transparencias.
# Calculos de subtotales por grupos
library(dplyr)##
## Attaching package: 'dplyr'## The following objects are masked from 'package:timeSeries':
##
## filter, lag## The following object is masked from 'package:kableExtra':
##
## group_rows## The following objects are masked from 'package:plyr':
##
## arrange, count, desc, failwith, id,
## mutate, rename, summarise, summarize## The following object is masked from 'package:car':
##
## recode## The following object is masked from 'package:neuralnet':
##
## compute## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union#dplyer biblioteca habilita la funcion %>%
#que nos permite cortar la línea de comando
#para que quepa en varios renglones.
# Survival status and Class
tit %>% group_by(Organismo, Exito) %>%
summarise(n = sum(Freq)) -> tit2d
alluvial(tit2d[,1:2], freq=tit2d$n, cex=0.5)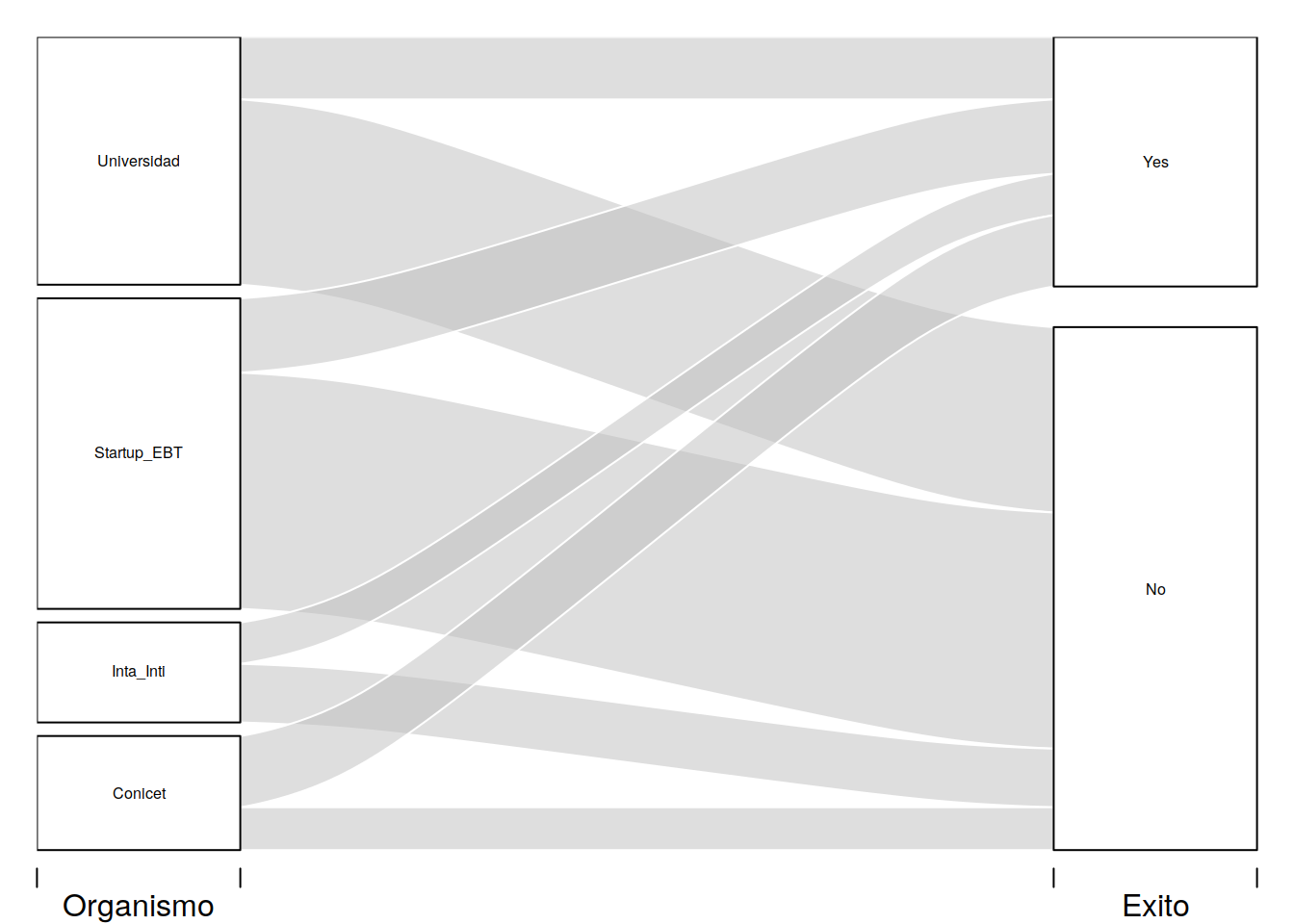
library(dplyr)
tit %>% group_by(APP, Sexo) %>%
summarise(n = sum(Monto)) -> tit2d
alluvial(tit2d[,1:2], freq=tit2d$n, cex= 0.5)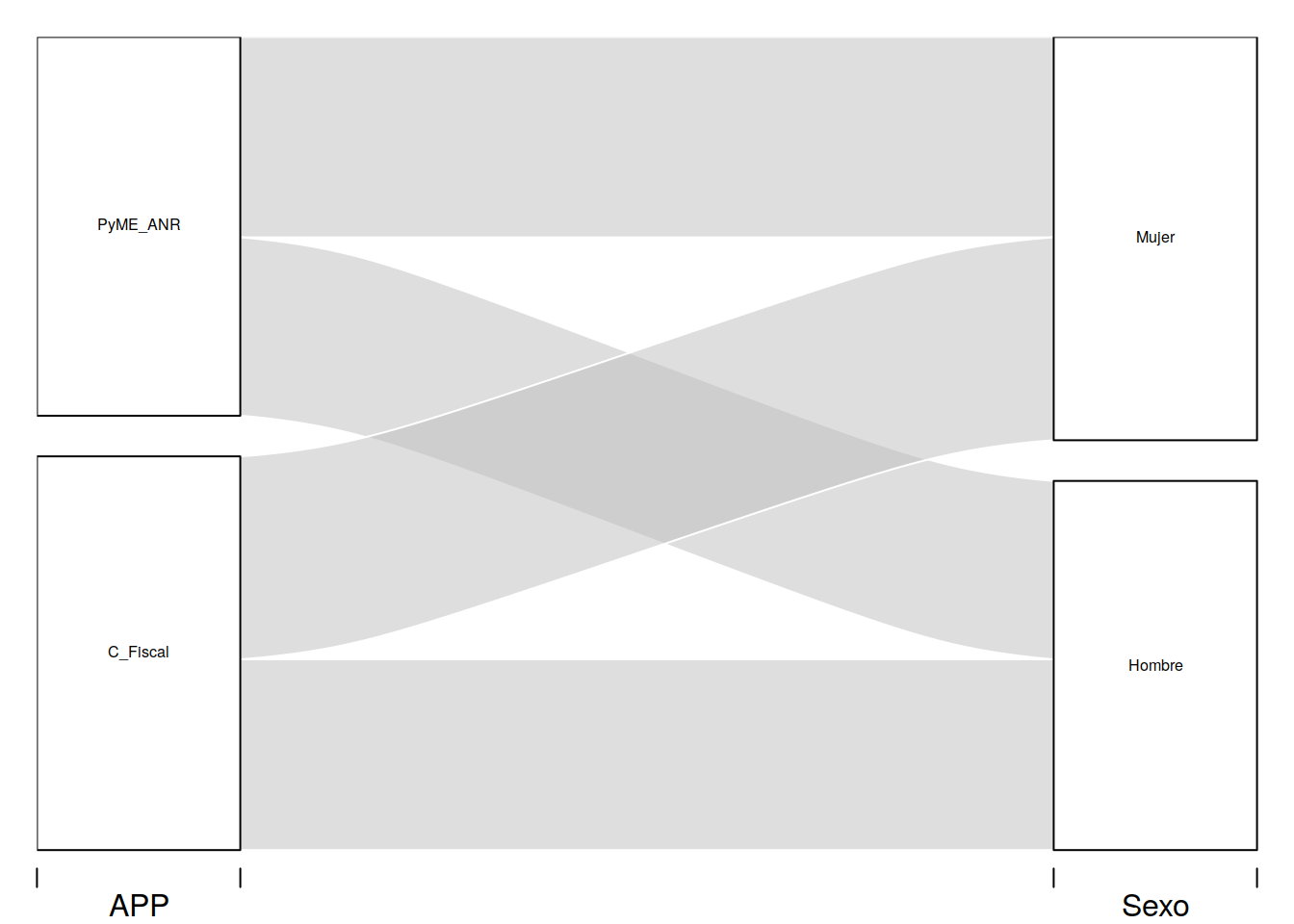
library(dplyr)
tit %>% group_by(Sexo, APP) %>%
summarise(n = sum(Freq)) -> tit2d
alluvial(tit2d[,1:2], freq=tit2d$n)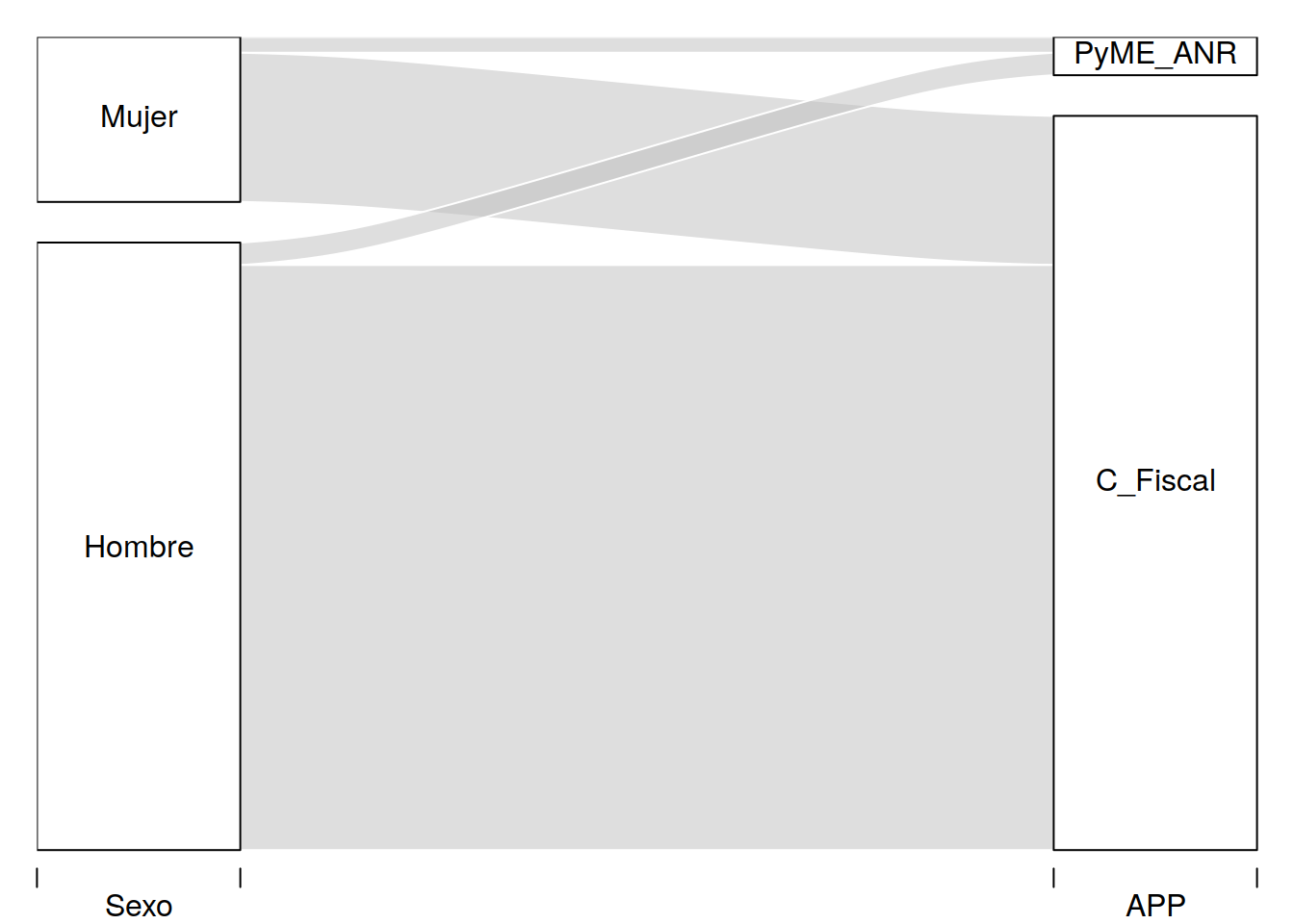
library(dplyr)
tit %>% group_by(Sexo, APP) %>%
summarise(n = sum(Monto)) -> tit2d
alluvial(tit2d[,1:2], freq=tit2d$n)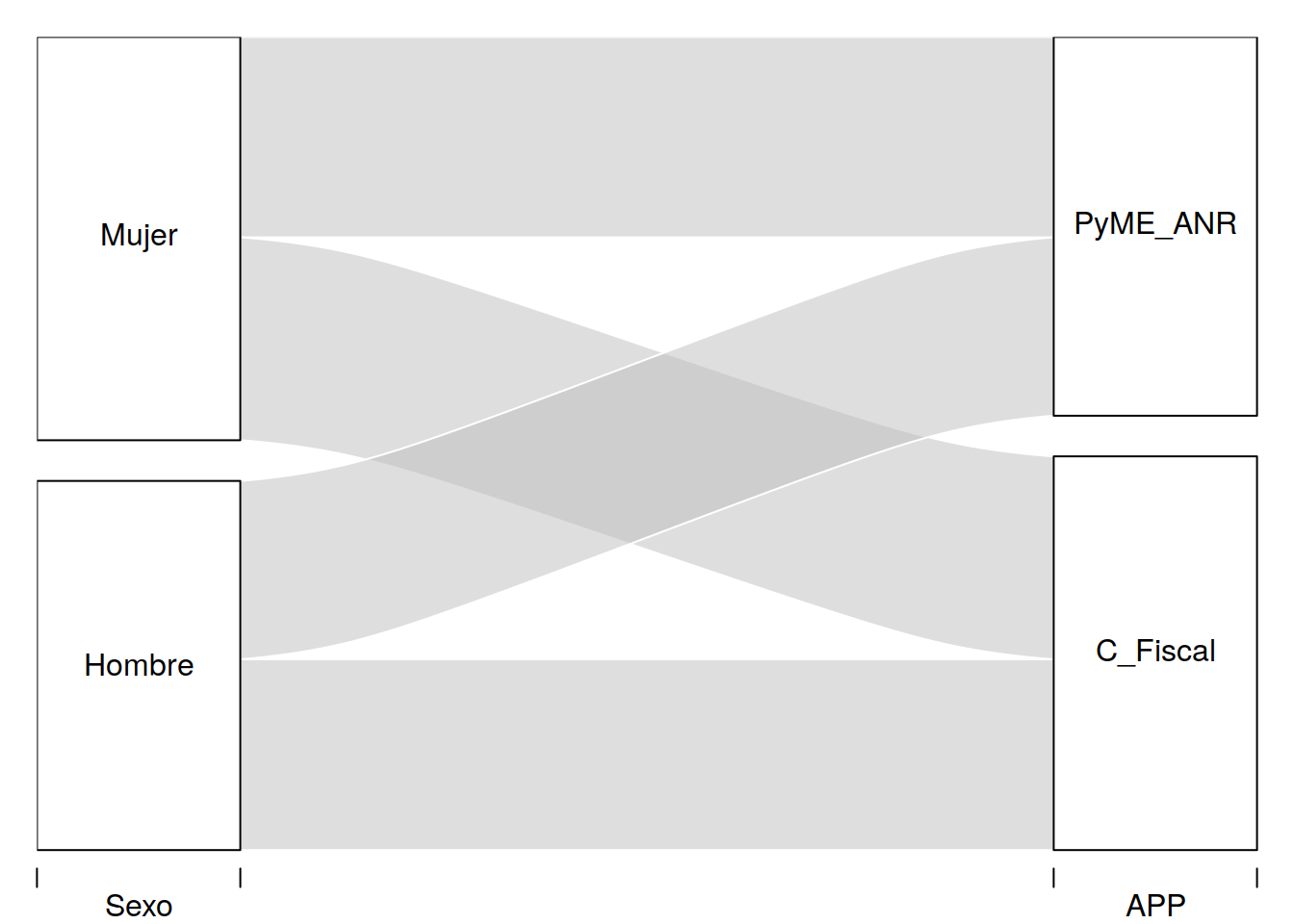
En este ejemplo hemos realizado el mismo ejemplo anterior pero en tres niveles. Hemos clasificado por sexo antes de las categorías anteriores.
Para graficar en orden inverso es necesario que consideremos armar nuevas categorías x e y que nos permitan partie de lo que antes era nuestro punto de llegada.
11.6 Árboles de Decisión (clasificación)
Los árboles de decisión son un método usado en distintas disciplinas como modelo de predicción. Estos son similares a diagramas de flujo, en los que llegamos a puntos en los que se toman decisiones de acuerdo a una regla.
En el campo del aprendizaje automático, hay distintas maneras de obtener árboles de decisión, la que usaremos en esta ocasión es conocida como CART: Classification And Regression Trees. Esta es una técnica de aprendizaje supervisado. Tenemos una variable objetivo (dependiente) y nuestra meta es obtener una función que nos permita predecir, a partir de variables predictoras (independientes), el valor de la variable objetivo para casos desconocidos.
Como el nombre indica, CART es una técnica con la que se pueden obtener árboles de clasificación y de regresión. Usamos clasificación cuando nuestra variable objetivo es discreta, mientras que usamos regresión cuando es continua. Nosotros tendremos una variable discreta, así que haremos clasificación.
La implementación particular de CART que usaremos es conocida como Recursive Partitioning and Regression Trees o RPART. De allí el nombre del paquete que utilizaremos en nuestro ejemplo.
De manera general, lo que hace este algoritmo es encontrar la variable independiente que mejor separa nuestros datos en grupos, que corresponden con las categorías de la variable objetivo. Esta mejor separación es expresada con una regla. A cada regla corresponde un nodo.
Por ejemplo, supongamos que nuestra variable objetivo tiene dos niveles, deudor y no deudor. Encontramos que la variable que mejor separa nuestros datos es ingreso mensual, y la regla resultante es que ingreso mensual > X pesos. Esto quiere decir que los datos para los que esta regla es verdadera, tienen más probabilidad de pertenecer a un grupo, que al otro. En este ejemplo, digamos que si la regla es verdadera, un caso tiene más probabilidad de formar parte del grupo no deudor.
Una vez hecho esto, los datos son separados (particionados) en grupos a partir de la regla obtenida. Después, para cada uno de los grupos resultantes, se repite el mismo proceso. Se busca la variable que mejor separa los datos en grupos, se obtiene una regla, y se separan los datos. Hacemos esto de manera recursiva hasta que nos es imposible obtener una mejor separación. Cuando esto ocurre, el algoritmo se detiene. Cuando un grupo no puede ser partido mejor, se le llama nodo terminal u hoja.
Una característica muy importante en este algoritmo es que una vez que alguna variable ha sido elegida para separar los datos, ya no es usada de nuevo en los grupos que ha creado. Se buscan variables distintas que mejoren la separación de los datos.
Además, supongamos después de una partición que hemos creado dos grupos, A y B. Es posible que para el grupo A, la variable que mejor separa estos datos sea diferente a la que mejor separa los datos en el grupo B. Una vez que los grupos se han separado, al algoritmo “no ve” lo que ocurre entre grupos, estos son independientes entre sí y las reglas que aplican para ellos no afectan en nada a los demás.
El resultado de todo el proceso anterior es una serie de bifurcaciones que tiene la apariencia de un árbol que va creciendo ramas, de allí el nombre del procedimiento (aunque a mí en realidad me parece más parecido a la raíz del árbol que a las ramas).
Las principales ventajas de este método son su interpretabilidad, pues nos da un conjunto de reglas a partir de las cuales se pueden tomar decisiones. Este es un algoritmo que no es demandante en poder de cómputo comparado con procedimientos más sofisticados y, a pesar de ello, que tiende a dar buenos resultados de predicción para muchos tipos de datos.
Sus principales desventajas son que este en tipo de clasificación “débil”, pues sus resultados pueden variar mucho dependiendo de la muestra de datos usados para entrenar un modelo. Además es fácil sobre ajustar los modelos, esto es, hacerlos excelentes para clasificar datos que conocemos, pero deficientes para datos conocidos.
Para saber más sobre este algoritmo, en particular que quiere decir eso de mejor separación, puedes leer el siguiente documento, que también llamar con la ayuda de R vignette(topic = "longintro", package = "rpart"):
https://cran.r-project.org/web/packages/rpart/vignettes/longintro.pdf
Ahora sí, empezamos preparando nuestro entorno de trabajo.
11.7 Uso de un árbol de decisión
** ¿Por qué puerto me conviene llegar a China?**
En este ejemplo cargaremos una tabla que indica los perfiles de las empresas y trataremos de explicar la columna "Empresa" o "Empresa Portuaria más conveniente" que indica por qué puerto de Chile envían sus productos a China.
Pretendemos que se nos entregue una arbol o método que sin muchas complicaciones nos diga la regla que debemos utilizar para seleccionar el puerto.
# La biblioteca party realiza el particionado recursivo
library(party)## Loading required package: grid## Loading required package: mvtnorm## Loading required package: modeltools## Loading required package: stats4##
## Attaching package: 'modeltools'## The following object is masked from 'package:fBasics':
##
## getModel## The following object is masked from 'package:plyr':
##
## empty## The following object is masked from 'package:car':
##
## Predict## Loading required package: strucchange## Loading required package: sandwichpartners <- read.table("Puertos_Chile.csv",header=TRUE,sep=",")
attach(partners)## The following object is masked from package:base:
##
## Fstr(partners) ## 'data.frame': 150 obs. of 6 variables:
## $ F : int 1 2 3 4 5 6 7 8 9 10 ...
## $ Tecnologia: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Normas : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Capital : num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Equipo : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Empresa : Factor w/ 3 levels "Iqui","S.Ant",..: 1 1 1 1 1 1 1 1 1 1 ...# Creamos una muestra para entrenar
ind <- sample(2, nrow(partners), replace=TRUE, prob=c(0.7, 0.3))
# toma una muestra
ind ## [1] 1 1 1 1 2 1 1 1 1 2 2 2 1 2 1 1 1 2 1 1 1 1
## [23] 1 1 2 2 1 2 1 1 1 1 1 2 1 1 1 1 2 1 1 1 1 1
## [45] 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2
## [67] 1 1 1 2 2 1 1 1 1 1 2 1 1 1 1 1 1 1 2 1 1 2
## [89] 1 1 1 1 1 2 1 2 1 1 1 1 1 1 1 2 2 1 1 2 1 1
## [111] 1 1 2 2 1 1 1 1 1 1 1 2 2 1 1 1 1 2 2 1 1 2
## [133] 1 2 1 1 1 1 2 2 1 1 1 2 1 1 1 1 2 2# nos imprime la muestra tomada.Hasta aquí no hay diferencias con lo que hemos hecho en regresión linela generalizada o en redes neuronales.
11.7.1 Entrenamiento del arbol
Crearemos un set de datos para engrenar y luego lo compararemos con los otros registros del set de datos original
library(party)
trainData <- partners [ind==1,]
# genero un set de entrenamiento
testData <- partners [ind==2,]
# genero un set de datos de prueba
myFormula <- Empresa ~ Tecnologia + Normas + Capital + Equipo
transit_ctree <- ctree(myFormula, data=trainData,) Haremos una predicciones y veremos la matriz de confusión
table(predict(transit_ctree), trainData$Empresa) ##
## Iqui S.Ant Valp
## Iqui 37 0 0
## S.Ant 0 30 0
## Valp 0 4 41print(transit_ctree) ##
## Conditional inference tree with 4 terminal nodes
##
## Response: Empresa
## Inputs: Tecnologia, Normas, Capital, Equipo
## Number of observations: 112
##
## 1) Capital <= 1.9; criterion = 1, statistic = 104.422
## 2)* weights = 37
## 1) Capital > 1.9
## 3) Equipo <= 1.7; criterion = 1, statistic = 51.099
## 4) Capital <= 4.7; criterion = 0.997, statistic = 11.487
## 5)* weights = 38
## 4) Capital > 4.7
## 6)* weights = 7
## 3) Equipo > 1.7
## 7)* weights = 3011.7.2 Nivel 1 del Árbol
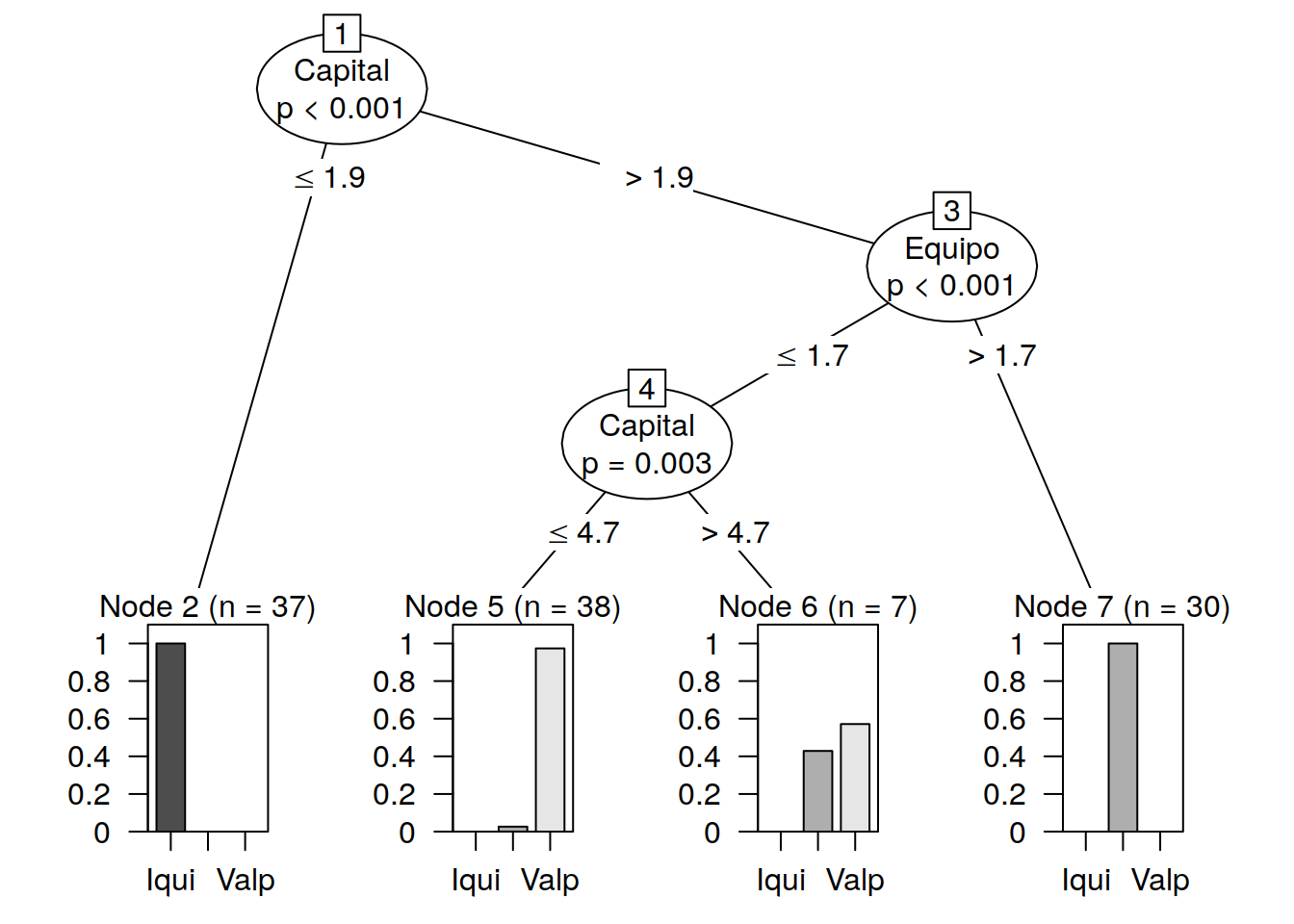
El arbol construido nos dice que para elegir un puerto lo primero que deberíamos ver es una comparación con el monto de capital. Si nnuestro capital es mayor o igual a 1.9 elijo Iquique.
Si mi capital es menor tengo que ir al segundo nivel y verificar mi Equipo
11.7.3 Nivel 2
Si el índice de equipo (tipo de camión) es mayor que 1.7 iré a San Antonio
En caso de Equipo igual o menor a 1.7 voy al nivel 3
11.7.4 Nivel 3
Vuelvo a observar el capital Si es mayoy o igual a 4.4 voy a Valparaíso Si es menor voy a San Antonio
11.7.5 Vista gráfica del arbol
plot(transit_ctree)