21 Aproximación de integrales
En este capítulo se mostrará cómo aproximar integrales en una y varias dimensiones.
21.1 Aproximación de Laplace unidimensional
Esta aproximación es útil para obtener el valor de una integral usando la expansión de Taylor para una función \(f(x)\) unimodal en \(\Re\), en otras palabras lo que interesa es: \[ I = \int_{-\infty}^{\infty} f(x) d(x)\] Al hacer una expansión de Taylor de segundo orden para \(\log(f(x))\) en su moda \(x_0\) el resultado es: \[ \log(f(x)) \approx \log(f(x_0)) + \frac{\log(f)^\prime(x_0)}{1!} (x-x_0) + \frac{\log(f)^{\prime \prime}(x_0)}{2!} (x-x_0)^2 \] El segundo término de la suma se anula porque \(\log(f)^\prime(x_0)=0\) por ser \(x_0\) el valor donde está el máximo de \(\log(f(x))\). La expresión anterior se simplifica en: \[ \log(f(x)) \approx \log(f(x_0)) + \frac{\log(f)^{\prime \prime}(x_0)}{2!} (x-x_0)^2 \] al aislar \(f(x)\) se tiene que
\[\begin{equation} \label{fx} f(x) \approx f(x_0) \exp \left( -\frac{c}{2} (x-x_0)^2 \right) \end{equation}\]
donde \(c=-\frac{d^2}{dx^2} \log(f(x)) \bigg|_{x=x_0}\).
La expresión se puede reescribir de manera que aparezca el núcleo de la función de densidad de la distribución normal con media \(x_0\) y varianza \(1/c\), a continuación la expresión
\[ f(x) \approx f(x_0) \frac{\sqrt{2 \pi / c}}{\sqrt{2 \pi / c}} \exp \left( -\frac{1}{2} \left( \frac{x-x_0}{1/\sqrt{c}} \right)^2 \right) \] Así al calcular la integral de \(f(x)\) en \(\Re\) se tiene que: \[\begin{equation} \label{aprox_laplace} I = \int_{-\infty}^{\infty} f(x) d(x) = f(x_0) \sqrt{2 \pi / c} \end{equation}\]
Ejemplo
Calcular la integral de \(f(x)=\exp \left( -(x-1.5)^2 \right)\) en \(\Re\) utilizando la aproximación de Laplace.
Primero vamos a dibujar la función \(f(x)\) para ver en dónde está su moda \(x_0\).
fun <- function(x) exp(-(x-1.5)^2)
curve(fun, from=-5, to=5, ylab='f(x)', las=1)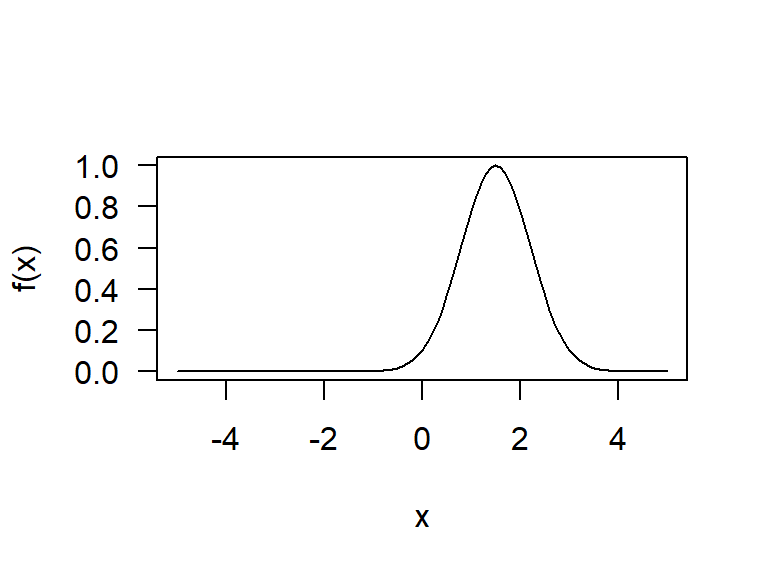
Figure 21.1: Perfil de la función f(x).
Visualmente se nota que la moda está cerca del valor 1.5 y para determinar numéricamente el valor de la moda \(x_0\) se usa la función optimize, los resultados se almacenan en el objeto res. El valor de la moda corresponde al elemento maximum del objeto res.
res <- optimize(fun, interval=c(-10, 10), maximum=TRUE)
res## $maximum
## [1] 1.499997
##
## $objective
## [1] 1Para determinar el valor de \(c\) de la expresión se utiliza el siguiente código.
require("numDeriv")
constant <- - as.numeric(hessian(fun, res$maximum))Para obtener la aproximación de la integral se usa la expresión y para tener un punto de comparación se evalua la integral usando la función integrate, a continuación el código.
fun(res$maximum) * sqrt(2*pi/constant)## [1] 1.772454integrate(fun, -Inf, Inf) # Para comparar## 1.772454 with absolute error < 1.5e-06De los anteriores resultados vemos que la aproximación es buena.