13 Medidas de correlación
En este capítulo se mostrará cómo obtener el coeficiente de correlación lineal para variables cuantitativas.
13.1 Función cor
La función cor permite calcular el coeficiente de correlación de Pearson, Kendall o Spearman para dos variables cuantitativas. La estructura de la función es la siguiente.
cor(x, y, use="everything",
method=c("pearson", "kendall", "spearman"))Los parámetos de la función son:
x, y: vectores cuantitativos.use: parámetro que indica lo que se debe hacer cuando se presenten registrosNAen alguno de los vectores. Las diferentes posibilidades son:everything,all.obs,complete.obs,na.or.completeypairwise.complete.obs, el valor por defecto eseverything.method: tipo de coeficiente de correlación a calcular, por defecto espearson, otros valores posibles sonkendallyspearman.
Ejemplo
Calcular el coeficiente de correlación de Pearson para las variables área y precio de la base de datos sobre apartamentos usados.
Lo primero que se debe hacer es cargar la base de datos usando la url apropiada. Luego de esto se usa la función cor sobre las variables de interés. A continuación se muestra el código necesario.
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/aptos2015'
datos <- read.table(file=url, header=T)
cor(x=datos$mt2, y=datos$precio)## [1] 0.8582585Del resultado anterior vemos que existe una correlación de 0.8582585 entre las dos variables, eso significa que apartamentos de mayor área tienden a tener precios de venta más alto. Este resultado se ilustra en la Figura 13.1, se nota claramente que la nube de puntos tiene un pendiente positiva y por eso el signo del coeficiente de correlación.
A continuación el código para generar la Figura 13.1.
with(datos, plot(x=mt2, y=precio, pch=20, col='blue',
xlab='Área del apartamento', las=1,
ylab='Precio del apartamento (millones COP)'))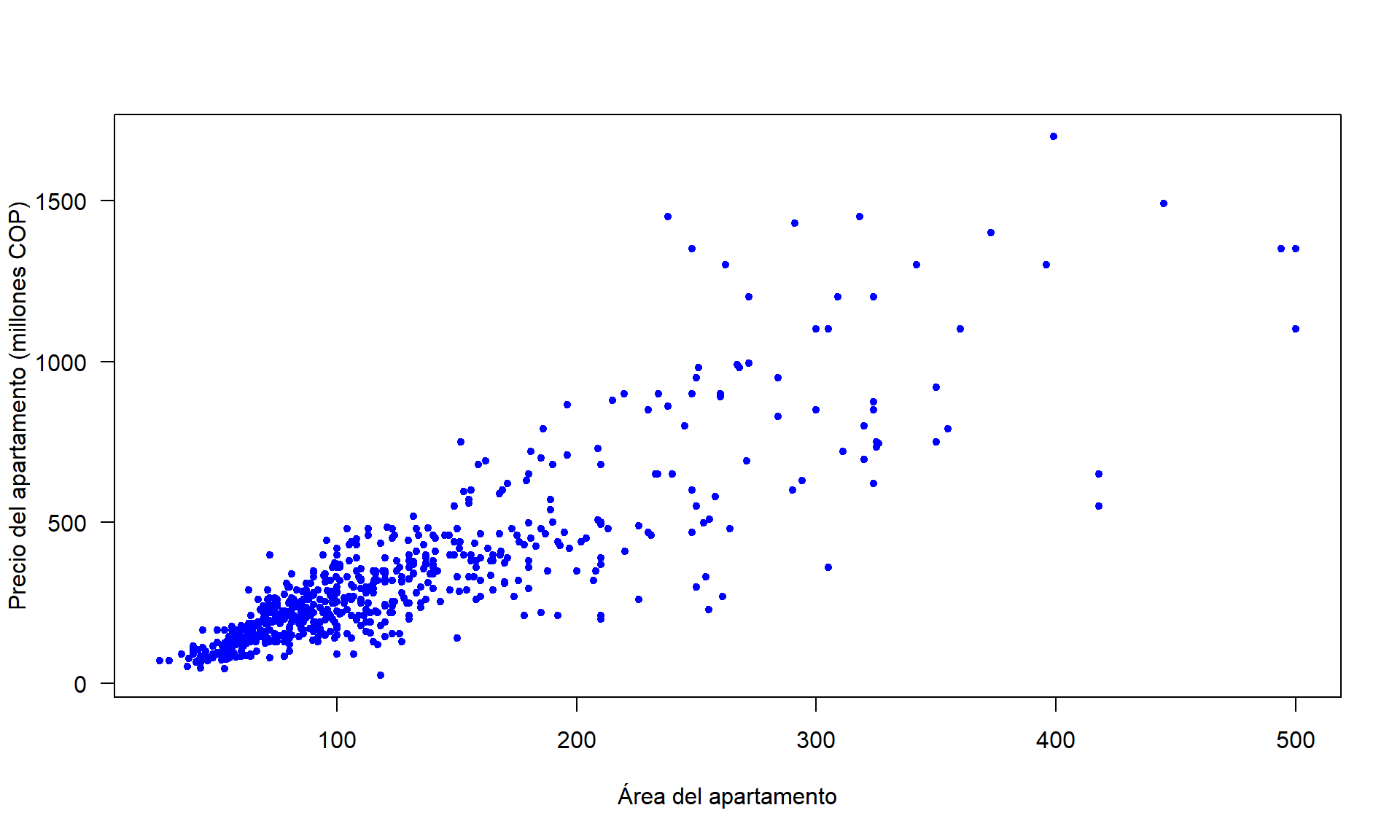
Figure 13.1: Diagrama de dispersión para precio versus área de los apartamentos usados.
Ejemplo
Para las mismas variables del ejemplo anterior calcular los coeficientes de correlación Kendall y Spearman.
A continuación el código para obtener lo solicitado.
cor(x=datos$mt2, y=datos$precio, method='pearson')## [1] 0.8582585cor(x=datos$mt2, y=datos$precio, method='kendall')## [1] 0.6911121cor(x=datos$mt2, y=datos$precio, method='spearman')## [1] 0.860306Ejemplo
Para la base de datos de apartamentos usados, ¿cuáles de las variables cuantitativas tienen mayor correlación?
Lo primero que debemos hacer es determinar cuáles son las cuantitativas de la base de datos. Para obtener información de las variables que están almacenadas en el marco de datos llamado datos usamos la función str que muestra la estructura interna de objeto.
str(datos)## 'data.frame': 694 obs. of 11 variables:
## $ precio : num 79 93 100 123 135 140 145 160 160 175 ...
## $ mt2 : num 43.2 56.9 66.4 61.9 89.8 ...
## $ ubicacion : chr "norte" "norte" "norte" "norte" ...
## $ estrato : int 3 2 3 2 4 3 3 3 4 4 ...
## $ alcobas : int 3 2 2 3 3 3 2 3 4 3 ...
## $ banos : int 1 1 2 2 2 2 2 2 2 2 ...
## $ balcon : chr "si" "si" "no" "si" ...
## $ parqueadero : chr "si" "si" "no" "si" ...
## $ administracion: num 0.05 0.069 0 0.13 0 0.12 0.14 0.127 0 0.123 ...
## $ avaluo : num 14.9 27 15.7 27 39.6 ...
## $ terminado : chr "no" "si" "no" "no" ...Del anterior resultado vemos que las variables precio, mt2, alcobas, banos, administracion y avaluo son las variables cuantitativas, las restantes son cualitativas (nominal u ordinal). Las posiciones de las variables cuantitativas en el objeto datos son 1, 2, 5, 6, 9, 10, así podemos construir un marco de datos sólo con la información cuantitativa, a continuación el código usado.
datos.cuanti <- datos[, c(1, 2, 5, 6, 9, 10)]
# La siguiente instrucción para editar los nombres de la variables
colnames(datos.cuanti) <- c('Precio', 'Área', 'Alcobas',
'Baños', 'Admon', 'Avaluo')
M <- round(cor(datos.cuanti), digits=2)
M## Precio Área Alcobas Baños Admon Avaluo
## Precio 1.00 0.86 0.19 0.63 0.75 0.79
## Área 0.86 1.00 0.31 0.67 0.77 0.75
## Alcobas 0.19 0.31 1.00 0.35 0.16 0.15
## Baños 0.63 0.67 0.35 1.00 0.55 0.53
## Admon 0.75 0.77 0.16 0.55 1.00 0.70
## Avaluo 0.79 0.75 0.15 0.53 0.70 1.00El anterior resultado representa la matriz de correlaciones entre las variables cuantitativas, se observa que la mayor correlación es entre las variables precio y área del apartamento.
Es posible representar gráficamente la matriz de correlaciones M por medio de la función corrplot del paquete corrplot (Wei and Simko 2017), a continuación el código para obtener su representación gráfica.
library('corrplot') # Para cargar el paquete corrplot## corrplot 0.84 loadedcorrplot.mixed(M)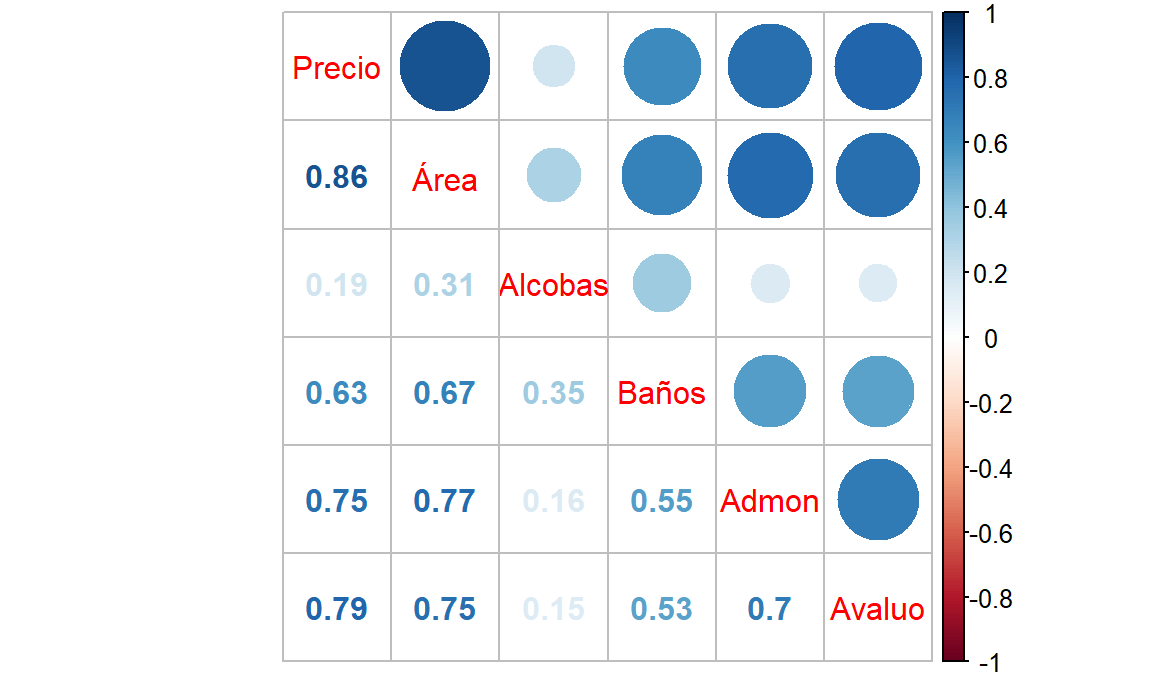
Figure 13.2: Matriz de coeficientes de correlación.
En la Figura 13.2 se muestra la matriz con los coeficientes de correlación. En la diagonal de la Figura 13.2 están las variables, por encima están unos círculos de colores, entre más intensidad del color, ya sea azul o rojo, mayor es la correlación, colores ténues significan correlación baja; el tamaño de los círculos está asociado al valor absoluto de correlación. Por debajo de la diagonal se observan los valores exactos de correlación en colores.
corrplot es muy versátil, se pueden obtener diferentes representaciones gráficas de la matriz de correlaciones, para conocer las diferentes posibilidades recomendamos consultar este enlace: https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html.
Ejemplo
Construya dos vectores hipotéticos con el gasto y ahorro de un grupo de 7 familias, incluya dos NA. Calcule el coeficiente de correlación entre ahorro y gasto, use el parámetro use para manejar los NA.
A continuación se presenta el código para crear los objetos ahorro y gasto con datos ficticios. Observe que en el primer caso donde se calcula la correlación no es posible obtener un resultado debido a que por defecto use='everything' y por lo tanto usa todas las observaciones incluyendo los NA. En el segundo caso si se obtiene un valor para la correlación debido a que se usó use='complete.obs'.
gasto <- c(170, 230, 120, 156, 256, NA, 352)
ahorro <- c(45, 30, NA, 35, 15, 65, 15)
cor(gasto, ahorro)## [1] NAcor(gasto, ahorro, use='complete.obs')## [1] -0.8465124EJERCICIOS
Use funciones o procedimientos (varias líneas) de R para responder cada una de las siguientes preguntas.
Para cada uno de los estratos socioeconómicos, calcular el coeficiente de correlación lineal de Pearson para las variables precio y área de la base de datos de los apartamentos usados.
Calcular los coeficientes de correlación Pearson, Kendall y Spearman para las variables cuantitativas de la base de datos sobre medidas del cuerpo explicada en el Capítulo 10. La url con la información es la siguiente: https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo
Represente gráficamente las matrices de correlación obtenidas en el ejercicio anterior.