19 Intervalos de confianza
En este capítulo se muestran las funciones que hay disponibles en R para construir intervalos de confianza para:
- la media \(\mu\),
- la proporción \(p\),
- la varianza \(\sigma^2\),
- la diferencia de medias \(\mu_1-\mu_2\) para muestras independientes y dependientes (o pareadas),
- la diferencia de proporciones \(p_1 - p_2\), y
- la razón de varianzas \(\sigma_1^2 / \sigma_2^2\).
Para ilustrar el uso de las funciones se utilizará la base de datos medidas del cuerpo presentada en el Capítulo 10.
19.1 Función t.test
La función t.test se usa para calcular intervalos de confianza para la media y diferencia de medias, con muestras independientes y dependientes (o pareadas). La función y sus argumentos son los siguientes:
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,
conf.level = 0.95, ...)19.1.1 Intervalo de confianza bilateral para la media \(\mu\)
Para calcular intervalos de confianza bilaterales para la media a partir de la función t.test es necesario definir 2 argumentos:
x: vector numérico con los datos.conf.level: nivel de confianza a usar, por defecto es 0.95.
Los demás argumentos se usan cuando se desea obtener intervalos de confianza para diferencia de media con muestras independientes y dependientes (o pareadas).
Ejemplo
Suponga que se quiere obtener un intervalo de confianza bilateral del 90% para la altura promedio de los hombres de la base de datos medidas del cuerpo.
Para calcular el intervalo de confianza, primero se carga la base de datos usando la url apropiada, luego se crea un subconjunto de datos y se aloja en el objeto hombres como sigue a continuación:
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]Una vez leídos los datos, se analiza la normalidad de la variable altura de los hombres, a partir de un QQplot y un histograma
par(mfrow=c(1, 2))
require(car) # Debe instalar antes el paquete car
qqPlot(hombres$altura, pch=19,
main='QQplot para la altura de hombres',
xlab='Cuantiles teóricos',
ylab='Cuantiles muestrales')## [1] 5 8hist(hombres$altura, freq=TRUE,
main='Histograma para la altura de hombres',
xlab='Altura (cm)',
ylab='Frecuencia')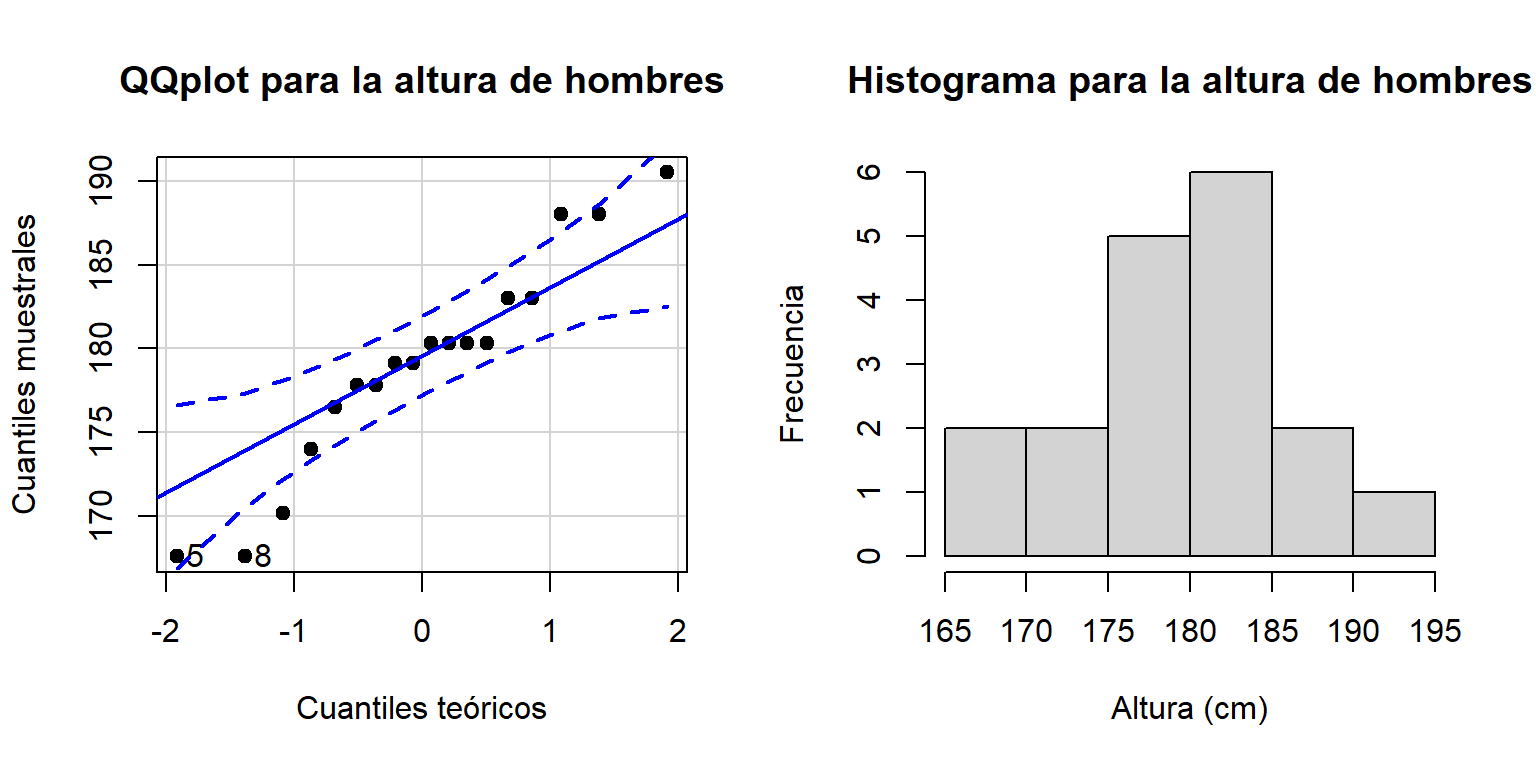
Figure 19.1: QQplot e histograma para la altura de los hombres.
En la Figura 19.1 se muestra el QQplot e histograma para la variable altura, de estas figuras no se observa un claro patrón normal, sin embargo, al aplicar la prueba Shapiro-Wilk a la muestra de alturas de los hombres se obtuvo un valor-P de 0.3599, por lo tanto, se asume que la muestra de alturas provienen de una población normal.
Una vez chequeado el supuesto de normalidad se puede usar la función t.test sobre la variable de interés para construir el intervalo de confianza. El resultado de usar t.test es una lista, uno de los elementos de esa lista es justamente el intevalo de confianza y para extraerlo es que se usa $conf.int al final de la instrucción. A continuación se muestra el código utilizado.
t.test(x=hombres$altura, conf.level=0.90)$conf.int## [1] 176.4384 181.7172
## attr(,"conf.level")
## [1] 0.9A partir del resultado obtenido se puede concluir, con un nivel de confianza del 90%, que la altura promedio de los estudiantes hombres se encuentra entre 176.4 cm y 181.7 cm.
19.1.2 Intervalo de confianza bilateral para la diferencia de medias (\(\mu_1-\mu_2\)) de muestras independientes
Para construir intervalos de confianza bilaterales para la diferencia de medias (\(\mu_1-\mu_2\)) de muestras independientes se usa la función t.test y es necesario definir 5 argumentos:
x: vector numérico con la información de la muestra 1,y: vector numérico con la información de la muestra 2,paired=FALSE: indica que el intervalo de confianza se hará para muestras independientes, en el caso de que sean dependientes (o pareadas) este argumento serápaired=TRUE,var.equal=FALSE: indica que las varianzas son desconocidas y diferentes, si la varianzas se pueden considerar iguales se colocavar.equal=TRUE.conf.level: nivel de confianza.
Ejemplo
Se quiere saber si existe diferencia estadísticamente significativa entre las alturas de los hombres y las mujeres. Para responder esto se va a construir un intervalo de confianza del \(95\%\) para la diferencia de las altura promedio de los hombres y de las mujeres (\(\mu_{hombres}-\mu_{mujeres}\)).
Para construir el intervalo de confianza, primero se carga la base de datos usando la url apropiada, luego se crean dos subconjuntos de datos y se alojan en los objetos hombres y mujeres como sigue a continuación:
url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]
mujeres <- datos[datos$sexo=="Mujer", ]Una vez leídos los datos, se analiza la normalidad de la variable altura de los hombres y las mujeres, a partir de un QQplot y un histograma
par(mfrow=c(2,2))
require(car) # Debe instalar antes el paquete car
qqPlot(hombres$altura, pch=19, las=1, main='QQplot',
xlab='Cuantiles teóricos', ylab='Cuantiles muestrales')## [1] 5 8hist(hombres$altura, las=1, xlab='Altura', ylab='Frecuencia',
main='Histograma para la altura de hombres')
qqPlot(mujeres$altura, pch=19, las=1, main='QQplot',
xlab='Cuantiles teóricos', ylab='Cuantiles muestrales')## [1] 16 9hist(mujeres$altura, las=1, xlab='Altura', ylab='Frecuencia',
main='Histograma para la altura de mujeres')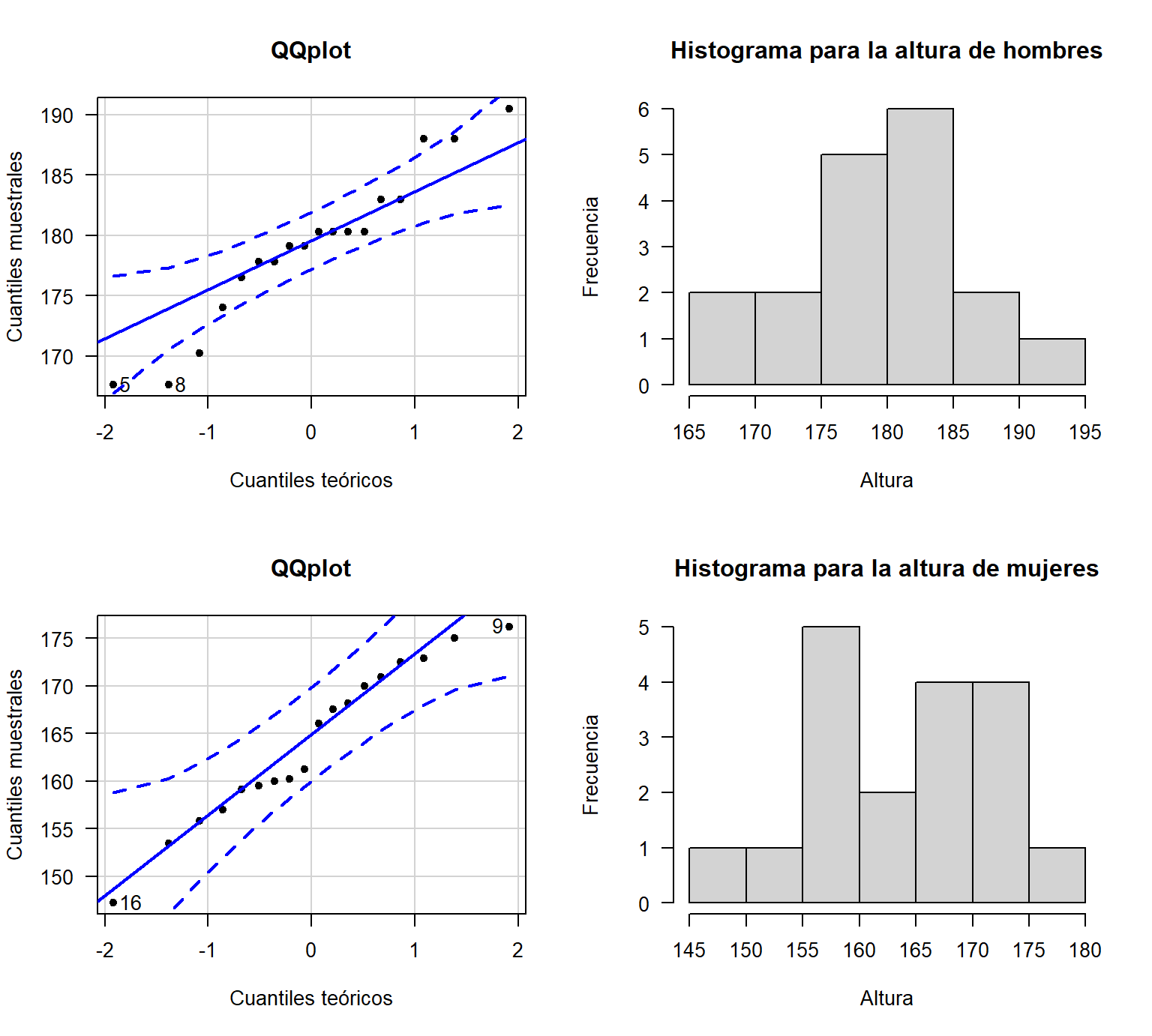
Figure 19.2: QQplot e histograma para la altura de hombres y mujeres.
De la Figura 19.2 se puede concluir que las alturas de los estudiantes hombres y mujeres siguen una distribución normal. Al aplicar la prueba Shapiro-Wilk para estudiar la normalidad de la altura se encontró un valor-P de 0.3599 para el grupo de hombres y un valor-P de 0.5921 para el grupo de mujeres, esto confirma que se cumple el supuesto de normalidad.
Como se cumple el supuesto de normalidad se puede usar la función t.test para construir el intervalo de confianza requerido. A continuación se muestra el código
t.test(x=hombres$altura, y=mujeres$altura,
paired=FALSE, var.equal=FALSE,
conf.level = 0.95)$conf.int## [1] 10.05574 20.03315
## attr(,"conf.level")
## [1] 0.95A partir del intervalo de confianza anterior se puede concluir, con un nivel de confianza del \(95\%\), que la altura promedio de los hombres es superior a la altura promedio de las mujeres, ya que el intervalo de confianza NO incluye el cero y por ser positivos sus limites se puede afirmar con un nivel de confianza del \(95\%\) que \(\mu_{hombres} > \mu_{mujeres}\).
19.1.3 Intervalo de confianza bilateral para la diferencia de medias (\(\mu_1-\mu_2\)) de muestras dependientes o pareadas
Para construir intervalos de confianza bilaterales para la diferencia de medias de muestras dependientes a partir de la función t.test es necesario definir 4 argumentos:
x: vector numérico con la información de la muestra 1,y: vector numérico con la información de la muestra 2,paired=TRUEindica que el intervalo de confianza se hará para muestras dependientes o pareadas.conf.level: nivel de confianza.
Ejemplo
Los desórdenes musculoesqueléticos del cuello y hombro son comunes entre empleados de oficina que realizan tareas repetitivas mediante pantallas de visualización. Se reportaron los datos de un estudio para determinar si condiciones de trabajo más variadas habrían tenido algún impacto en el movimiento del brazo. Los datos que siguen se obtuvieron de una muestra de \(n=16\) sujetos. Cada observación es la cantidad de tiempo, expresada como una proporción de tiempo total observado, durante el cual la elevación del brazo fue de menos de 30 grados. Las dos mediciones de cada sujeto se obtuvieron con una separación de 18 meses. Durante este período, las condiciones de trabajo cambiaron y se permitió que los sujetos realizaran una variedad más amplia de tareas. ¿Sugieren los datos que el tiempo promedio verdadero durante el cual la elevación es de menos de 30 grados luego del cambio difiere de lo que era antes? Calcular un intervalo de confianza del \(95\%\) para responder la pregunta.
| Sujeto | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Antes | 81 | 87 | 86 | 82 | 90 | 86 | 96 | 73 |
| Después | 78 | 91 | 78 | 78 | 84 | 67 | 92 | 70 |
| Diferencia | 3 | -4 | 8 | 4 | 6 | 19 | 4 | 3 |
| Sujeto | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|
| Antes | 74 | 75 | 72 | 80 | 66 | 72 | 56 | 82 |
| Después | 58 | 62 | 70 | 58 | 66 | 60 | 65 | 73 |
| Diferencia | 16 | 13 | 2 | 22 | 0 | 12 | -9 | 9 |
Para construir el intervalo de confianza primero se crean dos vectores con los datos y se nombran Antes y Despues, luego se calcula la diferencia y se aloja en el vector Diferencia, como sigue a continuación:
Antes <- c(81, 87, 86, 82, 90, 86, 96, 73,
74, 75, 72, 80, 66, 72, 56, 82)
Despues <- c(78, 91, 78, 78, 84, 67, 92, 70,
58, 62, 70, 58, 66, 60, 65, 73)
Diferencia <- Antes - DespuesEn seguida se analiza la normalidad de la variable Diferencia de los cambios en las condiciones de trabajo, a partir de un qqplot y una densidad.
par(mfrow=c(1,2))
require(car)
qqPlot(Diferencia, pch=19, main='QQplot para Diferencias', las=1,
xlab='Cuantiles teóricos', ylab='Cuantiles muestrales')## [1] 15 12plot(density(Diferencia), main='Densidad para Diferencias', las=1,
xlab='Diferencia de tiempo', ylab='Densidad')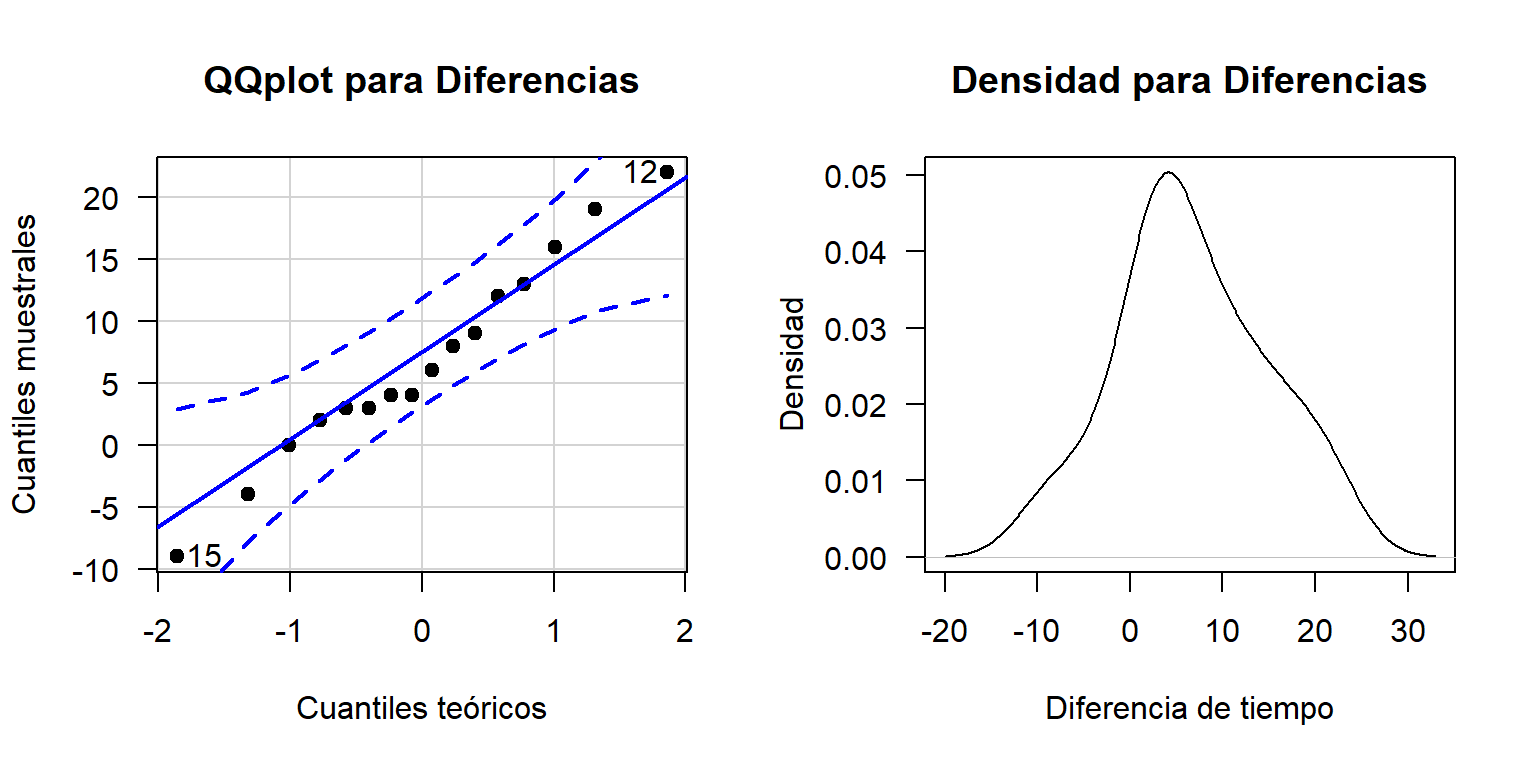
Figure 19.3: QQplot y densidad para Diferencias.
De la Figura 19.3 se observa que la diferencia de los tiempos sigue una distribución normal, debido a que en el QQplot se observa un patron lineal y la densidad muestra una forma cercana a la simétrica.
Luego de chequear la normalidad de la variable Diferencia se usa la función t.test para construir el intervalo. A continuación se muestra el código utilizado.
t.test(x=Antes, y=Despues, paired=TRUE, conf.level=0.95)$conf.int## [1] 2.362371 11.137629
## attr(,"conf.level")
## [1] 0.95A partir del resultado obtenido se puede concluir con un nivel de confianza del \(95\%\), que el tiempo promedio verdadero durante el cual la elevación es de menos de 30 grados luego del cambio difiere de lo que era antes del mismo. Como el intervalo de confianza es \(2.362< \mu_D < 11.138\), esto indica que \(\mu_{antes} - \mu_{despues}>0\) y por lo tanto \(\mu_{antes} > \mu_{despues}\).
19.1.4 Intervalo de confianza unilateral para la media \(\mu\)
Para construir intervalos de confianza unilaterales se usa el argumento alternative = 'less' o alternative='greater', a continuación un ejemplo.
Ejemplo
Simule una muestra aleatoria de una \(N(18, 3)\) y calcule un intervalo de confianza unilateral superior del \(90\%\) para la media
x <- rnorm(50, mean = 18, sd =3)
t.test(x, alternative = "greater", conf.level = 0.90)$conf.int## [1] 17.58728 Inf
## attr(,"conf.level")
## [1] 0.9En el resultado anterior se muestra el intervalo de confianza unilateral.
19.2 Función var.test
Para construir intervalos de confianza para la varianza se usa la función var.test del paquete stests (Hernandez 2020) disponible en el repositorio GitHub.
Para instalar el paquete stests desde GitHub se debe copiar el siguiente código en la consola de R:
if (!require('devtools')) install.packages('devtools')
devtools::install_github('fhernanb/stests', force=TRUE)Una vez instalado el paquete stests se puede usar la función var.test, la cual es una generalización de la función var.test del paquete stats y por esa razón aparece el siguiente mensaje en la consola cuando se invoca el paquete.
library(stests)
##
## The following object is masked from ‘package:stats’:
##
## var.testSi usted desea usar var.test del paquete stats o var.test del paquete stests, puede invocar las funciones explícitamente así:
stats::var.test() # Para usar la fución del paquete stats
stests::var.test() # Para usar la fución del paquete stestsstats::var.test() sólo sirve para 1 población.
- stests::var.test() sirve para 1 o 2 poblaciones.
19.2.1 Intervalo de confianza bilateral para la varianza \(\sigma^2\)
Para calcular intervalos de confianza bilaterales para la varianza \(\sigma^2\) a partir de la función var.test es necesario definir 2 argumentos:
x: vector numérico con la información de la muestra,conf.level: nivel de confianza.
Ejemplo
Considerando la información del ejemplo de Intervalos de confianza bilaterales para la media, construir un intervalo de confianza del 98% para la varianza de la altura de los estudiantes hombres.
require(stests) # Para cargar el paquete
res <- var.test(x=hombres$altura, conf.level=0.98)
res$conf.int## [1] 21.08468 109.93095
## attr(,"conf.level")
## [1] 0.98El intervalo de confianza del \(98\%\) indica que la varianza de la estatura de los estudiantes hombres se encuentra entre 21.08 y 109.93 \(cm^{2}\).
19.2.2 Intervalo de confianza bilateral para la razón de varianzas \(\sigma_1^2 / \sigma_2^2\)
Para calcular intervalos de confianza bilaterales para la razón de varianzas a partir de la función var.test es necesario definir 3 argumentos:
x: vector numérico con la información de la muestra 1,y: vector numérico con la información de la muestra 2,conf.level: nivel de confianza.
Ejemplo
Usando la información del ejemplo de diferencia de medias para muestras independientes se quiere obtener un intervalo de confianza del \(95\%\) para la razón de las varianzas de las alturas de los estudiantes hombres y mujeres.
var.test(x=hombres$altura, y=mujeres$altura,
conf.level=0.95)$conf.int## [1] 0.2327398 1.6632830
## attr(,"conf.level")
## [1] 0.95El intervalo de confianza del \(95\%\) indica que la razón de varianzas se encuentra entre 0.2327 y 1.6633. Puesto que el intervalo de confianza incluye el 1 se concluye que las varianzas de las alturas de los hombres y las mujeres son iguales.
¿Notó que las funciones var.test y var.test son diferentes?
var.test sirve para construir IC para \(\sigma^2\).
var.test sirve para construir IC para \(\sigma_1^2 / \sigma_2^2\).
19.3 Función prop.test
La función prop.test se usa para calcular intervalos de confianza para la porporción y diferencia de proporciones. La función y sus argumentos son los siguientes:
prop.test(x, n, p=NULL,
alternative=c("two.sided", "less", "greater"),
conf.level=0.95, correct=TRUE)19.3.1 Intervalo de confianza bilateral para la proporción \(p\)
Para calcular intervalos de confianza bilaterales para la proporción a partir de la función prop.test es necesario definir 3 argumentos: x considera el conteo de éxitos, n indica el número de eventos o de forma equivalente corresponde a la longitud de la variable que se quiere analizar, y conf.level corresponde al nivel de confianza.
Ejemplo
El gerente de una estación de televisión debe determinar en la ciudad qué porcentaje de casas tienen más de un televisor. Una muestra aleatoria de 500 casas revela que 275 tienen dos o más televisores. ¿Cuál es el intervalo de confianza del 90% para estimar la proporción de todas las casas que tienen dos o más televisores?
prop.test(x=275, n=500, conf.level=0.90)$conf.int## [1] 0.5122310 0.5872162
## attr(,"conf.level")
## [1] 0.9A partir del resultado obtenido se puede concluir, con un nivel de confianza del \(90\%\), que la proporción \(p\) de casas que tienen dos o más televisores se encuentra entre 0.5122 y 0.5872.
19.3.2 Intervalo de confianza bilateral para la diferencia de proporciones \(p_1 - p_2\)
Para construir intervalos de confianza bilaterales para la proporción a partir de la función prop.test es necesario definir 3 argumentos:
x: vector con el conteo de éxitos de las dos muestras,n: vector con el número de ensayos,conf.level: nivel de confianza.
Ejemplo
Se quiere determinar si un cambio en el método de fabricación de una piezas ha sido efectivo o no. Para esta comparación se tomaron 2 muestras, una antes y otra después del cambio en el proceso y los resultados obtenidos son los siguientes.
| Num piezas | Antes | Después |
|---|---|---|
| Defectuosas | 75 | 80 |
| Analizadas | 1500 | 2000 |
Construir un intervalo de confianza del 90% para decidir si el cambio tuvo efecto positivo o no.
prop.test(x=c(75, 80), n=c(1500, 2000), conf.level=0.90)$conf.int## [1] -0.002314573 0.022314573
## attr(,"conf.level")
## [1] 0.9A partir del resultado obtenido se puede concluir, con un nivel de confianza del \(90\%\), que la diferencia de proporción de defectos (\(p_1 - p_2\)) se encuentra entre -0.002315 y 0.022315. Como el cero está dentro del intervalo se concluye que el cambio en el método de fabricación no ha disminuído el porcentaje de defectos.