20 Prueba de hipótesis
En este capítulo se muestran las funciones que hay disponibles en R para realizar prueba de hipótesis para:
- la media \(\mu\),
- la proporción \(p\),
- la varianza \(\sigma^2\),
- la diferencia de medias \(\mu_1-\mu_2\) para muestras independientes y dependientes (o pareadas),
- la diferencia de proporciones \(p_1 - p_2\), y
- la razón de varianzas \(\sigma_1^2 / \sigma_2^2\).
20.1 Prueba de hipótesis para \(\mu\) de una población normal
Para realizar este tipo de prueba se puede usar la función t.test que tiene la siguiente estructura.
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,
conf.level = 0.95, ...)Los argumentos a definir dentro de t.test para hacer la prueba son:
x: vector numérico con los datos.alternative: tipo de hipótesis alterna. Los valores disponibles son"two.sided"cuando la hipótesis alterna es \(\neq\),"less"para el caso \(<\) y"greater"para \(>\).mu: valor de referencia de la prueba.conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).
Ejemplo
Para verificar si el proceso de llenado de bolsas de café con 500 gramos está operando correctamente se toman aleatoriamente muestras de tamaño diez cada cuatro horas. Una muestra de bolsas está compuesta por las siguientes observaciones: 502, 501, 497, 491, 496, 501, 502, 500, 489, 490.
¿Está el proceso llenando bolsas conforme lo dice la envoltura? Use un nivel de significancia del 5%.
Solución
Lo primero es explorar si la muestra proviene de una distribución normal, para eso ingresamos los datos y aplicamos la prueba Anderson-Darling por medio de la función ad.test disponible en el paquete nortest (Gross and Ligges 2015) como se muestra a continuación.
contenido <- c(510, 492, 494, 498, 492,
496, 502, 491, 507, 496)
require(nortest) # Se debe haber instalado antes nortest
ad.test(contenido)##
## Anderson-Darling normality test
##
## data: contenido
## A = 0.49161, p-value = 0.1665Como el valor-P de la prueba Anderson-Darling es 20% y mayor que el nivel de significancia del 5%, se puede asumir que la muestra proviene de una población normal.
Luego de haber explorado la normalidad retornamos al problema de interés que se puede resumir así:
\[H_0: \mu = 500 \quad gr\]
\[H_1: \mu \neq 500 \quad gr\]
La prueba de hipótesis se puede realizar usando la función t.test por medio del siguiente código.
t.test(contenido, alternative='two.sided',
conf.level=0.95, mu=500)##
## One Sample t-test
##
## data: contenido
## t = -1.0629, df = 9, p-value = 0.3155
## alternative hypothesis: true mean is not equal to 500
## 95 percent confidence interval:
## 493.1176 502.4824
## sample estimates:
## mean of x
## 497.8Como el valor-P es 30% y mayor que el nivel de significancia 5%, no se rechaza la hipótesis nula, es decir, las evidencias no son suficientes para afirmar que el proceso de llenando no está cumpliendo con lo impreso en la envoltura.
20.2 Prueba de hipótesis para \(\mu\) con muestras grandes
Ejemplo
Se afirma que los automóviles recorren en promedio más de 20000 kilómetros por año pero usted cree que el promedio es en realidad menor. Para probar tal afirmación se pide a una muestra de 100 propietarios de automóviles seleccionada de manera aleatoria que lleven un registro de los kilómetros que recorren.
¿Estaría usted de acuerdo con la afirmación si la muestra aleatoria indicara un promedio de 19500 kilómetros y una desviación estándar de 3900 kilómetros? Utilice un valor P en su conclusión y use una significancia del 3%.
Solución
En este problema interesa:
\[H_0: \mu \ge 20000 \quad km\] \[H_1: \mu < 20000 \quad km\] Para este tipo de pruebas no hay una función de R que haga los cálculos, por esta razón uno mismo debe escribir una líneas de código para obtener los resultados deseados, a continuación las instrucciones para calcular el estadístico y su valor-P.
xbarra <- 19500 # Datos del problema
desvia <- 3900 # Datos del problema
n <- 100 # Datos del problema
mu <- 20000 # Media de referencia
est <- (xbarra - mu) / (desvia / sqrt(n))
est # Para obtener el valor del estadístico## [1] -1.282051pnorm(est) # Para obtener el valor-P## [1] 0.09991233Como el valor-P es mayor que el nivel de significancia 3%, no hay evidencias suficientes para pensar que ha disminuido el recorrido anual promedio de los autos.
20.3 Prueba de hipótesis para la proporción \(p\)
Existen varias pruebas para estudiar la propoción \(p\) de una distribución binomial, a continuación el listado de las más comunes.
- Prueba de Wald,
- Prueba \(\Chi^2\) de Pearson,
- Prueba binomial exacta.
20.3.1 Prueba de Wald
Esta prueba se recomienda usar cuando se tiene un tamaño de muestra \(n\) suficientemente grande para poder usar la distribución normal para aproximar la distribución binomial.
En esta prueba el estadístico está dado por
\[z=\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}},\] donde \(\hat{p}\) es la proporción muestral calculada como el cociente entre el número de éxitos \(x\) observados en los \(n\) ensayos y \(p_0\) es el valor de referencia de las hipótesis. El estadístico \(z\) tiene distribución \(N(0, 1)\) cuando \(n \to \infty\).
Para realizar esta prueba en R no hay una función y debemos escribir la líneas de código para obtener el estadístico y el valor-P de la prueba. A continuación se muestra un ejemplo de cómo proceder para aplicar la prueba de Wald.
Ejemplo
Un fabricante de un quitamanchas afirma que su producto quita 90% de todas las manchas. Para poner a prueba esta afirmación se toman 200 camisetas manchadas de las cuales a solo 174 les desapareció la mancha. Pruebe la afirmación del fabricante a un nivel \(\alpha=0.05\).
Solución
En este problema interesa probar lo siguiente:
\[H_0: p = 0.90\] \[H_1: p < 0.90\]
Del anterior conjunto de hipótesis se observa que el valor de referencia de la prueba es \(p_0=0.90\). De la información inicial se tiene que de las \(n=200\) pruebas se observó que en \(x=174\) la mancha desapareció, con esta información se puede calcular el estadístico \(z\) así:
z <- (174/200 - 0.90) / sqrt(0.90 * (1 - 0.90) / 200)
z # Para obtener el valor del estadístico## [1] -1.414214Para obtener el valor-P de la prueba debemos tener en cuenta el sentido en la hipótesis alternativa \(H_1: p < 0.90\), por esa razón el valor-P será \(P(Z<z)\) y para obtenerlo usamos el siguiente código
pnorm(q=z, lower.tail=TRUE) # Para obtener el valor-P## [1] 0.0786496El valor-P obtenido se puede representar gráficamente en la Figura 20.1.
Como el valor-P obtenido fue mayor que el nivel de significancia \(\alpha=0.05\) se concluye que no hay evidencias suficientes para rechazar la hipótesis nula.
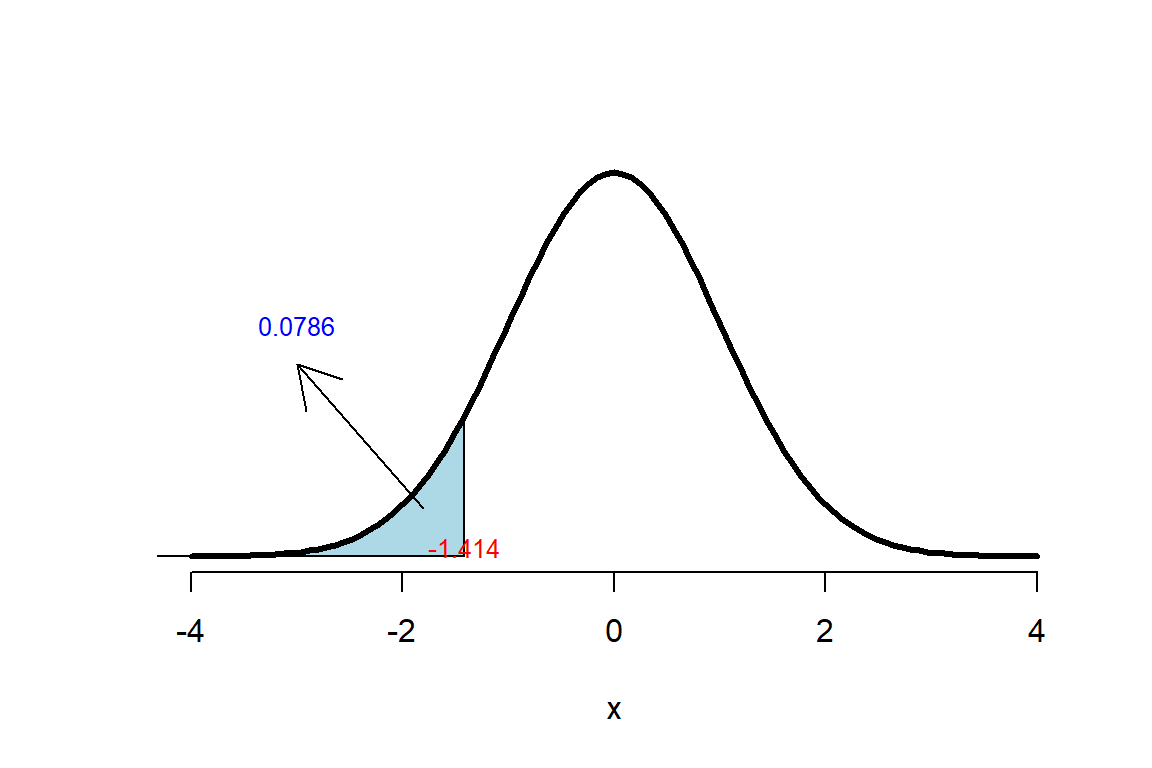
Figure 20.1: Representación del Valor-P para la prueba Wald.
20.3.2 Prueba \(\Chi^2\) de Pearson
Para realizar la prueba \(\Chi^2\) de Pearson se usa la función prop.test que tiene la siguiente estructura.
prop.test(x, n, p = NULL,
alternative = c("two.sided", "less", "greater"),
conf.level = 0.95, correct = TRUE)Los argumentos a definir dentro de prop.test para hacer la prueba son:
x: número de éxitos en la muestra.n: número de observaciones en la muestra.alternative: tipo de hipótesis alterna. Los valores disponibles son"two.sided"cuando la alterna es \(\neq\),"less"para el caso \(<\) y"greater"para \(>\).p: valor de referencia de la prueba.correct: valor lógico para indicar si se usa la corrección de Yates.conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).
Ejemplo
Un fabricante de un quitamanchas afirma que su producto quita 90% de todas las manchas. Para poner a prueba esta afirmación se toman 200 camisetas manchadas de las cuales a solo 174 les desapareció la mancha. Pruebe la afirmación del fabricante a un nivel \(\alpha=0.05\).
Solución
En este problema interesa probar lo siguiente:
\[H_0: p = 0.90\]
\[H_1: p < 0.90\]
La forma de usar la función prop.test para realizar la prueba se muestra a continuación.
prop.test(x=174, n=200, p=0.9, alternative='less',
conf.level=0.95, correct=FALSE)##
## 1-sample proportions test without continuity correction
##
## data: 174 out of 200, null probability 0.9
## X-squared = 2, df = 1, p-value = 0.07865
## alternative hypothesis: true p is less than 0.9
## 95 percent confidence interval:
## 0.0000000 0.9042273
## sample estimates:
## p
## 0.87Como el valor-P (con valor de 0.07865 pero repotado en la salida como 0.08) es mayor que \(\alpha\) no se rechaza la hipótesis nula y se concluye que no hay evidencias suficientes para rechazar la hipótesis nula.
20.3.3 Prueba binomial exacta
Para realizar la prueba binomial exacta se usa la función binom.test que tiene la siguiente estructura.
binom.test(x, n, p = 0.5,
alternative = c("two.sided", "less", "greater"),
conf.level = 0.95)Los argumentos a definir dentro de binom.test para hacer la prueba son:
x: número de éxitos en la muestra.n: número de observaciones en la muestra.alternative: tipo de hipótesis alterna. Los valores disponibles son"two.sided"cuando la alterna es \(\neq\),"less"para el caso \(<\) y"greater"para \(>\).p: valor de referencia de la prueba.conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).
Ejemplo
Un asadero de pollos asegura que 90% de sus órdenes se entregan en menos de 10 minutos. En una muestra de 20 órdenes, 17 se entregaron dentro de ese lapso. ¿Puede concluirse en el nivel de significancia 0.05, que menos de 90% de las órdenes se entregan en menos de 10 minutos?
Solución
En este problema interesa probar lo siguiente:
\[H_0: p = 0.90\]
\[H_1: p < 0.90\]
La forma de usar la función binom.test para realizar la prueba se muestra a continuación.
binom.test(x=17, n=20, p=0.9, alternative="less")##
## Exact binomial test
##
## data: 17 and 20
## number of successes = 17, number of trials = 20, p-value = 0.3231
## alternative hypothesis: true probability of success is less than 0.9
## 95 percent confidence interval:
## 0.0000000 0.9578306
## sample estimates:
## probability of success
## 0.85Como el valor-P (reportado como 0.3 pero con valor de 0.3231) es mayor que \(\alpha\) no se rechaza la hipótesis nula y se concluye que no hay evidencias suficientes para rechazar la hipótesis nula.
20.4 Prueba de hipótesis para la varianza \(\sigma^2\) de una población normal
Para realizar este tipo de prueba se usa la función var.test del paquete usefultools (Hernandez 2020) disponible en el repositorio GitHub. La función var.test tiene la siguiente estructura.
var.test(x, alternative = "two.sided",
null.value = 1, conf.level = 0.95)Los argumentos a definir dentro de var.test para hacer la prueba son:
x: vector numérico con los datos.alternative: tipo de hipótesis alterna. Los valores disponibles son"two.sided"cuando la alterna es \(\neq\),"less"para el caso \(<\) y"greater"para \(>\).null.value: valor de referencia de la prueba.conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).
Para instalar el paquete usefultools desde GitHub se debe copiar el siguiente código en la consola de R:
if (!require('devtools')) install.packages('devtools')
devtools::install_github('fhernanb/usefultools', force=TRUE)Ejemplo
Para verificar si el proceso de llenado de bolsas de café está operando con la variabilidad permitida se toman aleatoriamente muestras de tamaño diez cada cuatro horas. Una muestra de bolsas está compuesta por las siguientes observaciones: 502, 501, 497, 491, 496, 501, 502, 500, 489, 490. El proceso de llenado está bajo control si presenta un varianza de 40 o menos. ¿Está el proceso llenando bolsas conforme lo dice la envoltura? Use un nivel de significancia del 5%.
Solución
En un ejemplo anterior se comprobó que la muestra proviene de una población normal así que se puede proceder con la prueba de hipótesis sobre \(\sigma^2\).
En este ejemplo nos interesa estudiar el siguiente conjunto de hipótesis
\[H_0: \sigma^2 \leq 40\]
\[H_1: \sigma^2 > 40\]
La prueba de hipótesis se puede realizar usando la función var.test por medio del siguiente código.
contenido <- c(510, 492, 494, 498, 492,
496, 502, 491, 507, 496)
require(usefultools) # Ya debe estar instalado
var.test(x=contenido, alternative='greater',
null.value=40, conf.level=0.95)##
## X-squared test for variance
##
## data: contenido
## X-squared = 9.64, df = 9, p-value = 0.3804
## alternative hypothesis: true variance is greater than 40
## 95 percent confidence interval:
## 0.000 115.966
## sample estimates:
## variance of x
## 42.84444Como el valor-P es mayor que el nivel de significancia 5%, no se rechaza la hipótesis nula, es decir, las evidencias no son suficientes para afirmar que la varianza del proceso de llenado es mayor que 40 unidades.
20.5 Prueba de hipótesis para el cociente de varianzas \(\sigma_1^2 / \sigma_2^2\)
Para realizar este tipo de prueba se puede usar la función var.test.
Ejemplo
Se realiza un estudio para comparar dos tratamientos que se aplicarán a frijoles crudos con el objetivo de reducir el tiempo de cocción. El tratamiento T1 es a base de bicarbonato de sodio, el T2 es a base de cloruro de sodio o sal común. La variable respuesta es el tiempo de cocción en minutos. Los datos se muestran abajo. ¿Son las varianzas de los tiempos iguales o diferentes? Usar \(\alpha=0.05\).
T1: 76, 85, 74, 78, 82, 75, 82.
T2: 57, 67, 55, 64, 61, 63, 63.
Solución
En este problema interesa probar si las varianzas poblacionales son iguales o no, por esta razón el cociente de \(\sigma_{T1}^2 / \sigma_{T2}^2\) se iguala al valor de 1 que será el valor de referencia de la prueba.
\[H_0: \sigma_{T1}^2 / \sigma_{T2}^2 = 1\] \[H_1: \sigma_{T1}^2 / \sigma_{T2}^2 \neq 1\]
Para ingresar los datos se hace lo siguiente:
T1 <- c(76, 85, 74,78, 82, 75, 82)
T2 <- c(57, 67, 55, 64, 61, 63, 63)Primero se debe explorar si las muestras provienen de una población normal y para esto se construyen los QQplot que se muestran en la Figura 20.2, a continuación el código para generar la Figura 20.2.
q1 <- qqnorm(T1, plot.it=FALSE)
q2 <- qqnorm(T2, plot.it=FALSE)
plot(range(q1$x, q2$x), range(q1$y, q2$y), type="n", las=1,
xlab='Theoretical Quantiles', ylab='Sample Quantiles')
points(q1, pch=19)
points(q2, col="red", pch=19)
qqline(T1, lty='dashed')
qqline(T2, col="red", lty="dashed")
legend('topleft', legend=c('T1', 'T2'), bty='n',
col=c('black', 'red'), pch=19)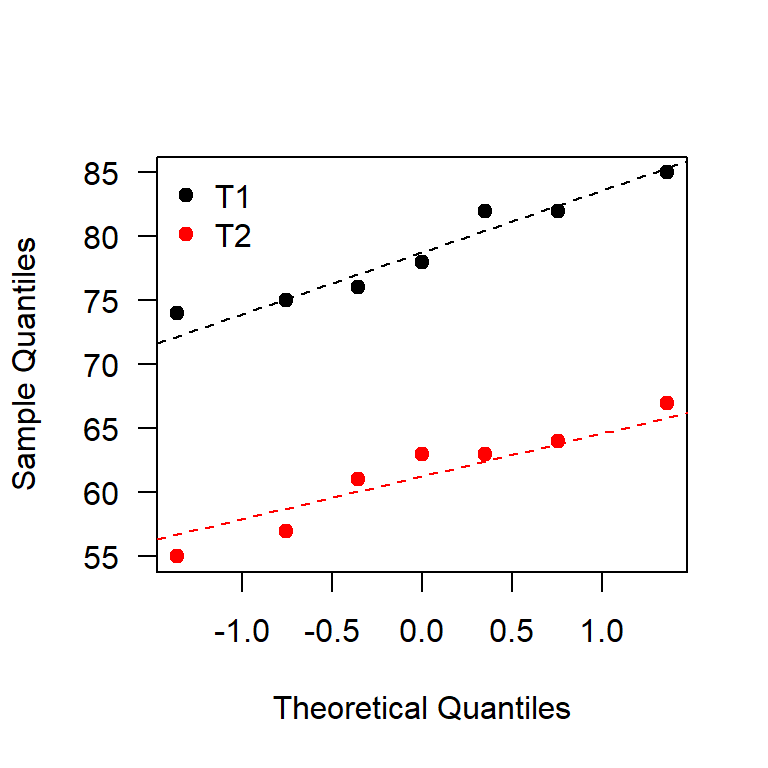
Figure 20.2: QQplot para los tiempos de cocción.
De la Figura 20.2 se observa que los puntos están bastante alineados lo cual nos lleva a pensar que las muestras si provienen de una población normal, para estar más seguros se aplicará una prueba formal para estudiar la normalidad.
A continuación el código para aplicar la prueba de normalidad Kolmogorov-Smirnov a cada una de las muestras.
require(nortest) # Se debe tener instalado
lillie.test(T1)$p.value## [1] 0.520505lillie.test(T2)$p.value## [1] 0.3952748Del QQplot mostrado en la Figura 20.2 y las pruebas de normalidad se observa que se puede asumir que las poblaciones son normales.
La función var.test se puede usar para probar \(H_0\), a continuación el código para realizar la prueba.
var.test(T1, T2, null.value=1, alternative="two.sided",
conf.level=0.95)##
## F test to compare two variances
##
## data: T1 and T2
## F = 1.011, num df = 6, denom df = 6, p-value = 0.9897
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.1737219 5.8838861
## sample estimates:
## ratio of variances
## 1.011019Como el valor-P es 0.9897 (reportado como 1 en la salida anterior), muy superior al nivel \(\alpha\) de significancia 5%, se puede concluir que las varianzas son similares.
Ejemplo
El arsénico en agua potable es un posible riesgo para la salud. Un artículo reciente reportó concentraciones de arsénico en agua potable en partes por billón (ppb) para diez comunidades urbanas y diez comunidades rurales. Los datos son los siguientes:
Urbana: 3, 7, 25, 10, 15, 6, 12, 25, 15, 7
Rural: 48, 44, 40, 38, 33, 21, 20, 12, 1, 18
Solución
¿Son las varianzas de las concentraciones iguales o diferentes? Usar \(\alpha=0.05\).
En este problema interesa probar:
\[H_0: \sigma_{Urb}^2 / \sigma_{Rur}^2 = 1\] \[H_1: \sigma_{Urb}^2 / \sigma_{Rur}^2 \neq 1\]
Para ingresar los datos se hace lo siguiente:
urb <- c(3, 7, 25, 10, 15, 6, 12, 25, 15, 7)
rur <- c(48, 44, 40, 38, 33, 21, 20, 12, 1, 18)Primero se debe explorar si las muestras provienen de una población normal, para esto se construyen los QQplot mostrados en la Figura 20.3.
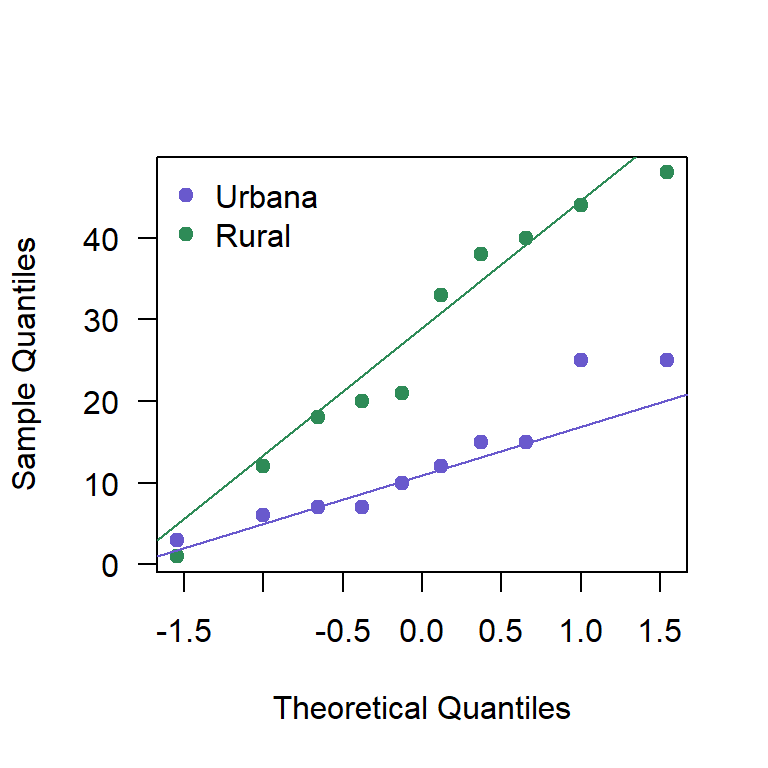
Figure 20.3: QQplot para las concentraciones de arsénico.
A continuación el código para aplicar la prueba de normalidad Kolmogorov-Smirnov, a continuación el código usado.
require(nortest) # Se debe tener instalado
lillie.test(urb)$p.value## [1] 0.5522105lillie.test(rur)$p.value## [1] 0.6249628Del QQplot mostrado en la Figura 20.3 y las pruebas de normalidad se observa que se pueden asumir poblaciones normales.
La función var.test se puede usar para probar \(H_0\), a continuación el código para realizar la prueba.
var.test(urb, rur, null.value=1, alternative="two.sided",
conf.level=0.95)##
## F test to compare two variances
##
## data: urb and rur
## F = 0.24735, num df = 9, denom df = 9, p-value = 0.04936
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.06143758 0.99581888
## sample estimates:
## ratio of variances
## 0.2473473Como el valor-P es 0.0493604 (reportado como 0.05 en la salida anterior) y es menor que el nivel de significancia \(\alpha=0.05\), se puede concluir que las varianzas no son iguales.
¿Notó que las funciones var.test y var.test son diferentes?
var.test sirve para prueba de hipótesis sobre \(\sigma^2\).
var.test sirve para prueba de hipótesis sobre \(\sigma_1^2 / \sigma_2^2\).
20.6 Prueba de hipótesis para la diferencia de medias \(\mu_1-\mu_2\) con varianzas iguales
Para realizar este tipo de prueba se puede usar la función t.test que tiene la siguiente estructura.
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,
conf.level = 0.95, ...)Los argumentos a definir dentro de t.test para hacer la prueba son:
x: vector numérico con la información de la muestra 1,y: vector numérico con la información de la muestra 2,alternative: tipo de hipótesis alterna. Los valores disponibles son"two.sided"cuando la alterna es \(\neq\),"less"para el caso \(<\) y"greater"para \(>\).mu: valor de referencia de la prueba.var.equal=TRUE: indica que las varianzas son desconocidas pero iguales.conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).
Ejemplo
Retomando el ejemplo de los fríjoles, ¿existen diferencias entre los tiempos de cocción de los fríjoles con T1 y T2? Usar un nivel de significancia del 5%.
Primero se construirá un boxplot comparativo para los tiempos de cocción diferenciando por el tratamiento que recibieron. Abajo el código para obtener en este caso el boxplot. En la Figura 20.4 se muestra el boxplot, de esta figura se observa que las cajas de los boxplot no se traslapan, esto es un indicio de que las medias poblacionales, \(\mu_1\) y \(\mu_2\), son diferentes, se observa también que el boxplot para el tratamiento T1 está por encima del T2.
datos <- data.frame(tiempo=c(T1, T2), trat=rep(1:2, each=7))
boxplot(tiempo ~ trat, data=datos, las=1,
xlab='Tratamiento', ylab='Tiempo (min)')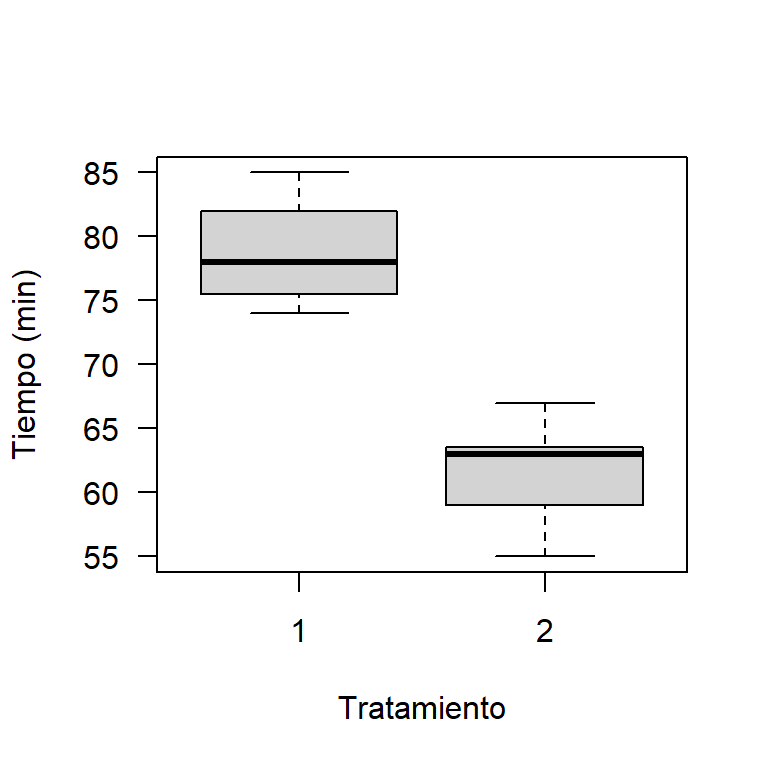
Figure 20.4: Boxplot para los tiempos de cocción dado el tratamiento.
En este problema interesa estudiar el siguiente conjunto de hipótesis.
\[H_0: \mu_1 - \mu_2 = 0\] \[H_1: \mu_1 - \mu_2 \neq 0\]
El código para realizar la prueba es el siguiente:
t.test(x=T1, y=T2, alternative="two.sided", mu=0,
paired=FALSE, var.equal=TRUE, conf.level=0.97)##
## Two Sample t-test
##
## data: T1 and T2
## t = 7.8209, df = 12, p-value = 4.737e-06
## alternative hypothesis: true difference in means is not equal to 0
## 97 percent confidence interval:
## 11.94503 22.91212
## sample estimates:
## mean of x mean of y
## 78.85714 61.42857De la prueba se obtiene un valor-P muy pequeño, por lo tanto, podemos concluir que si hay diferencias significativas entre los tiempos promedios de cocción con T1 y T2, resultado que ya se sospechaba al observar la Figura 20.4.
Si el objetivo fuese elegir el tratamiento que minimice los tiempos de cocción se recomendaría el tratamiento T2, remojo de fríjoles en agua con sal.
20.7 Prueba de hipótesis para la diferencia de medias \(\mu_1-\mu_2\) con varianzas diferentes
Ejemplo
Retomando el ejemplo de la concentración de arsénico en el agua, ¿existen diferencias entre las concentraciones de arsénico de la zona urbana y rural? Usar un nivel de significancia del 5%.
Primero se construirá un boxplot comparativo para las concentraciones de arsénico diferenciando por la zona donde se tomaron las muestras. Abajo el código para obtener en este caso el boxplot. En la Figura 20.5 se muestra el boxplot, de esta figura se observa que las cajas de los boxplot no se traslapan, esto es un indicio de que las medias poblacionales, \(\mu_1\) y \(\mu_2\), son diferentes, se observa también que el boxplot para la zona rural está por encima del de la zona urbana.
datos <- data.frame(Concentracion=c(urb, rur),
Zona=rep(c('Urbana', 'Rural'), each=10))
boxplot(Concentracion ~ Zona, data=datos, las=1,
xlab='Zona', ylab='Concentración arsénico (ppb)')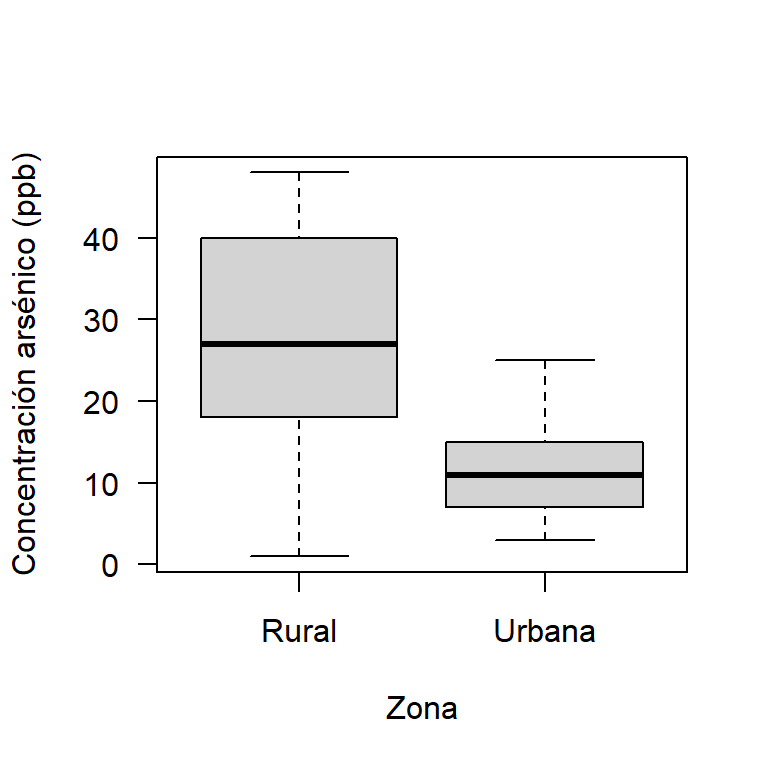
Figure 20.5: Boxplot para las concentaciones de arsénico dada la zona.
En este problema interesa estudiar el siguiente conjunto de hipótesis.
\[H_0: \mu_1 - \mu_2 = 0\] \[H_1: \mu_1 - \mu_2 \neq 0\]
El código para realizar la prueba es el siguiente:
t.test(x=urb, y=rur, alternative="two.sided", mu=0,
paired=FALSE, var.equal=FALSE, conf.level=0.95)##
## Welch Two Sample t-test
##
## data: urb and rur
## t = -2.7669, df = 13.196, p-value = 0.01583
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -26.694067 -3.305933
## sample estimates:
## mean of x mean of y
## 12.5 27.5De la prueba se obtiene un valor-P pequeño, por lo tanto, podemos concluir que si hay diferencias significativas entre las concentraciones de arsénico del agua entre las dos zonas, resultado que ya se sospechaba al observar la Figura 20.5. La zona que presenta mayor concentración media de arsénico en el agua es la rural.
20.8 Prueba de hipótesis para la diferencia de proporciones \(p_1 - p_2\)
Para realizar pruebas de hipótesis para la proporción se usa la función prop.test y es necesario definir los siguientes argumentos:
x: vector con el conteo de éxitos de las dos muestras,n: vector con el número de ensayos de las dos muestras,alternative: tipo de hipótesis alterna. Los valores disponibles son"two.sided"cuando la alterna es \(\neq\),"less"para el caso \(<\) y"greater"para \(>\).p: valor de referencia de la prueba.conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).
Ejemplo
Se quiere determinar si un cambio en el método de fabricación de una piezas ha sido efectivo o no. Para esta comparación se tomaron 2 muestras, una antes y otra después del cambio en el proceso y los resultados obtenidos son los siguientes.
| Num piezas | Antes | Después |
|---|---|---|
| Defectuosas | 75 | 80 |
| Analizadas | 1500 | 2000 |
Realizar una prueba de hipótesis con un nivel de significancia del 10%.
En este problema interesa estudiar el siguiente conjunto de hipótesis.
\[H_0: p_{antes} - p_{despues} = 0\] \[H_1: p_{antes} - p_{despues} > 0\]
Para realizar la prueba se usa la función prop.test como se muestra a continuación.
prop.test(x=c(75, 80), n=c(1500, 2000),
alternative='greater', conf.level=0.90)##
## 2-sample test for equality of proportions with continuity correction
##
## data: c(75, 80) out of c(1500, 2000)
## X-squared = 1.7958, df = 1, p-value = 0.09011
## alternative hypothesis: greater
## 90 percent confidence interval:
## 0.0002765293 1.0000000000
## sample estimates:
## prop 1 prop 2
## 0.05 0.04Del reporte anterior se observa que el Valor-P es 9%, por lo tanto no hay evidencias suficientes para pensar que el porcentaje de defectuosos después del cambio ha disminuído.
20.9 Prueba de hipótesis para la diferencia de medias pareadas
Ejemplo
Diez individuos participaron de programa para perder peso corporal por medio de una dieta. Los voluntarios fueron pesados antes y después de haber participado del programa y los datos en libras aparecen abajo. ¿Hay evidencia que soporte la afirmación de la dieta disminuye el peso medio de los participantes? Usar nivel de significancia del 5%.
| Sujeto | 001 002 003 004 005 006 007 008 009 010 |
|---|---|
| Antes | 195 213 247 201 187 210 215 246 294 310 |
| Después | 187 195 221 190 175 197 199 221 278 285 |
Primero se debe explorar si las diferencias de peso (antes-después) provienen de una población normal, para esto se construye el QQplot mostrado en la Figura 20.6. De la figura no se observa un alejamiento serio de la recta de referencia, por lo tanto se puede asumir que las diferencias se distribuyen en forma aproximadamente normal.
antes <- c(195, 213, 247, 201, 187, 210, 215, 246, 294, 310)
despu <- c(187, 195, 221, 190, 175, 197, 199, 221, 278, 285)
dif <- antes - despu
qqnorm(dif, pch=19, main='')
qqline(dif)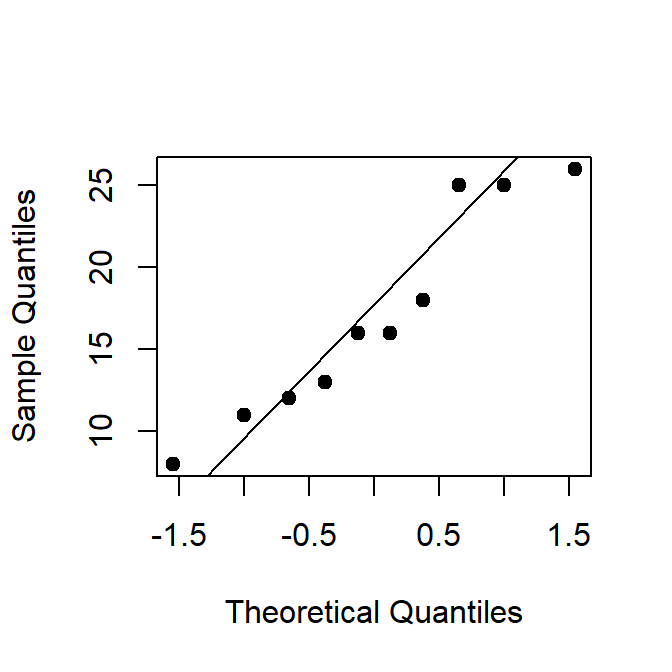
Figure 20.6: QQplot para las diferencias de peso.
Se puede aplicar la prueba de normalidad Kolmogorov-Smirnov para estudiar si las diferencias dif provienen de una población normal, esto se puede realizar por medio del siguiente código.
require(nortest)
lillie.test(dif)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: dif
## D = 0.19393, p-value = 0.3552De la salida anterior se observa que el valor-P de la prueba es grande por lo tanto se puede asumir que las diferencias se distribuyen en forma aproximadamente normal.
En este problema interesa estudiar el siguiente conjunto de hipótesis.
\[H_0: \mu_{antes} - \mu_{despues} = 0\] \[H_1: \mu_{antes} - \mu_{despues} > 0\]
El código para realizar la prueba es el siguiente:
t.test(x=antes, y=despu, alternative="greater", mu=0,
paired=TRUE, conf.level=0.95)##
## Paired t-test
##
## data: antes and despu
## t = 8.3843, df = 9, p-value = 7.593e-06
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
## 13.2832 Inf
## sample estimates:
## mean of the differences
## 17De la prueba se obtiene un valor-P pequeño, por lo tanto, podemos concluir que el peso \(\mu_{antes}\) es mayor que \(\mu_{despues}\), en otras palabras, la dieta si ayudó a disminuir el peso corporal.