10 Gestión del Riesgo
10.1 Definiciones:
RIESGO, AMENAZA, EXPOSICIÓN Y VULNERABILIDAD.
Una forma sencilla de entender el Riesgo, la Amenaza, la Exposición y la Vulnerabilidad es mediante el enfoque que una investigadora del CONICET propuesto por Celeste Saulo mailto:csaulo@smn.gov.ar. La profesora Saulo proviene del campo disciplinar de las ciencias de la atmosfera, más precisamente del sub campo de la metoerología. En este campo el uso de las estadísticas y R-Cran son pan de todos los días. En sus trabajos de investigación ella aborda el problema del riesgo, pensando en los eventos climáticos extremos, fundamentalmente como consecuencia del cambio climático. En su comunidad y sobre todo por sus interacciones con el IPCC adopta (se apropia) del marco teórico que ellos utilizan, pero le propone al Gobierno Argnetino utilizar esta metodología para abordar cualquier problema de riesgo. En la actualidad la profesora Saulo es directora del Servicio Meteorológico Nacional de Argentina.
En 2019, la señora Celeste Saulo fue elegida por el Decimoctavo Congreso Meteorológico Mundial para desempeñar el cargo de Primera Vicepresidenta de la Organización Meteorológica Mundial (OMM) durante un mandato de cuatro años que empezó inmediatamente después de la clausura del Congreso. Previamente, había ejercido en calidad de Segunda Vicepresidenta y Primera Vicepresidenta interina de la Organización.
En el plan estratégico del Servicio Meteorológico Nacional se lee "el interés que se tiene por el desarrollo y articulación en los pronósticos de largo alcance para el planeamiento y misiones logísticas de envergadura".
Este es un campo promisorio para desarrollar tesis multidisciplinarias doctorales.
10.1.1 Dsiminuir Riesgo = Aumentar la Certidumbre
La mejor solución para disminuir los riesgos en el país es la adaptación, lo anterior implica evaluar el riesgo climático en las comunidades que es la combinación de un evento, su posibilidad y sus consecuencias. Cuando una amenaza se materializa en un evento, el riesgo se convierte en un desastre y esto se traduce en impactos socio económicos.
\[RIESGO=f (AMENAZA, EXPOSICIÓN, VULNERABILIDAD)\]
Los habitantes de una comunidad, sus cultivos, casas, escuelas, acueductos, están en contacto con fenómenos climáticos, como: sequías, lluvias, vientos, huracanes, esto se define como Exposición.
Pero, si en el camino de un fenómeno climático como torrenciales lluvias, se encuentra con elementos expuestos como los cultivos, las casas, las carreteras, los medios de transporte de una comunidad específica, esto se convierte en una amenaza que podría afectar, la vida de las comunidades, su economía e infraestructura. Cuando una amenaza se materializa en un evento, el riesgo se convierte en un desastre que se traduce en impactos socio-económicos y ambientales. La Vulnerabilidad Es la predisposición que tiene un sistema de ser afectado de forma negativa ante una amenaza. La sensibilidad del sistema es la predisposición de las comunidades, la infraestructura o un ecosistema de ser afectado por una amenaza debido a sus condiciones. La capacidad de adaptación, son las acciones y medidas encaminadas a reducir la vulnerabilidad de los sistemas naturales y humanos ante los efectos reales o esperados del cambio climático. Anticipar, resistir, acomodarse y recuperarse de un evento climatológico es adaptarse; al aumentar la capacidad adaptativa de las comunidades, disminuye su vulnerabilidad y esto se refleja en la disminución de los daños ante los eventos climáticos. RIESGO CLIMÁTICO El riesgo climático es la probabilidad de pérdidas socioeconómicas y de ecosistemas por eventos climatológicos, lo que se traduce en la evaluación de la exposición, la amenaza y la vulnerabilidad. Para evaluar estos factores se deben tener en cuenta los efectos climáticos que han afectado a la comunidad en los últimos años y evaluar como las lluvia, las sequías y los vientos, han impactado a las comunidades y su infraestructura además de la evaluación de las afectaciones a los ecosistemas; a partir de lo anterior se planean las acciones de adaptación.
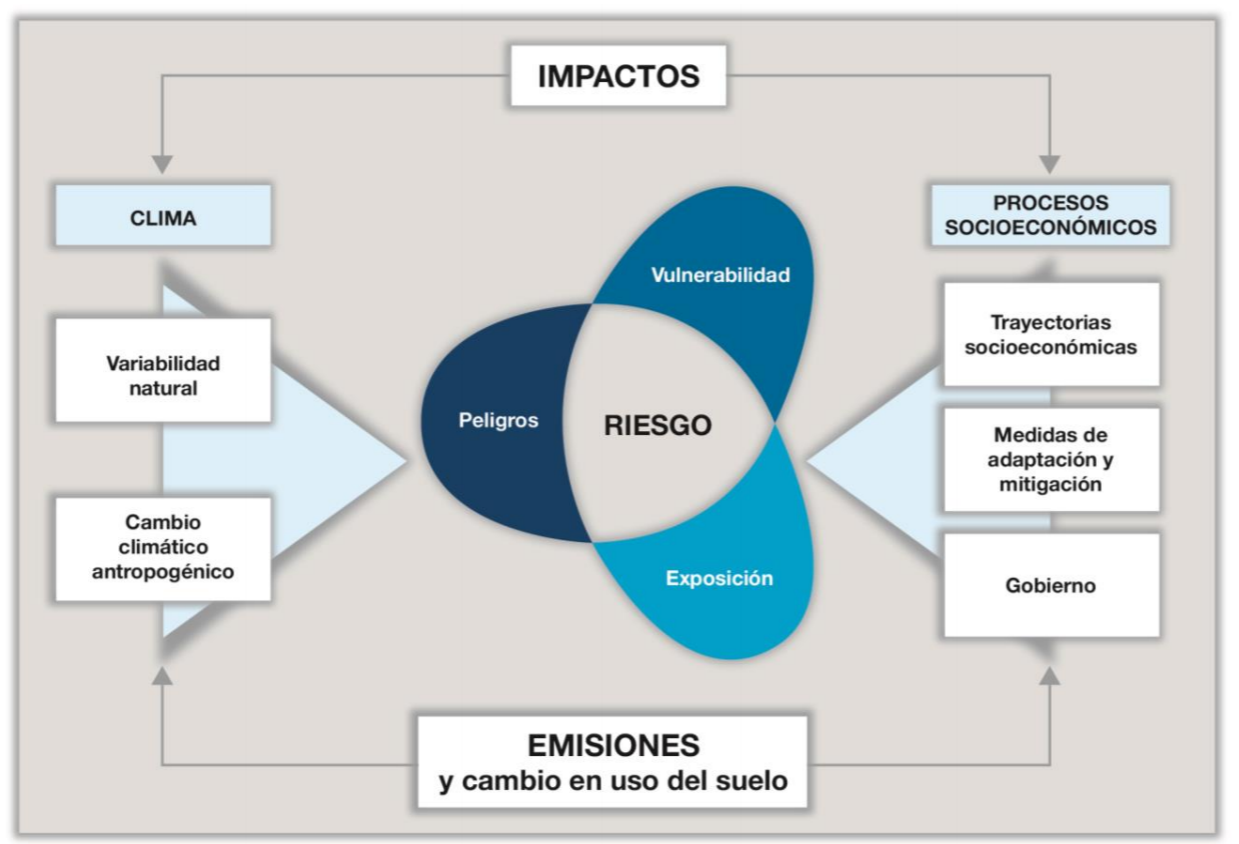
Flujograma de Gestión del Riesgo
10.2 KNN
En casos de incidentes desconocidos, o nunca antes experimentados, siempre podremos conseguir recurrir a la historia y la geografía para encontrar un caso parecido al nuestro. Para ello es necesario contar con una nube de datos que nos permita encontrar el caso semejante al nuestro. En ayuda nuestra surge la técnica del Knn.
10.2.1 Kesimo Vecino Más Próximo
Es una técnica de agrupamiento
Separa a los datos en grupos (entrenamiento)
Si vengo con un caso nuevo me dice como quien se va a comportar10.2.2 Cargar datos frontera pareto
library(readr)
datos <- read_csv("https://themys.sid.uncu.edu.ar/rpalma/R-cran/risk_tir.csv")## Parsed with column specification:
## cols(
## VAN = col_double(),
## RISK = col_double()
## )Leer Riesgo VAN del decimo valor
datos[10,2]## # A tibble: 1 x 1
## RISK
## <dbl>
## 1 25.8datos[10,1]## # A tibble: 1 x 1
## VAN
## <dbl>
## 1 691135.Polteo Datos
mx <- -datos$RISK
my <- datos$VAN
plot(mx,my,type="p", main="Frontera Pareto en Mendoza",ylab="VAN",xlab="Riesgo")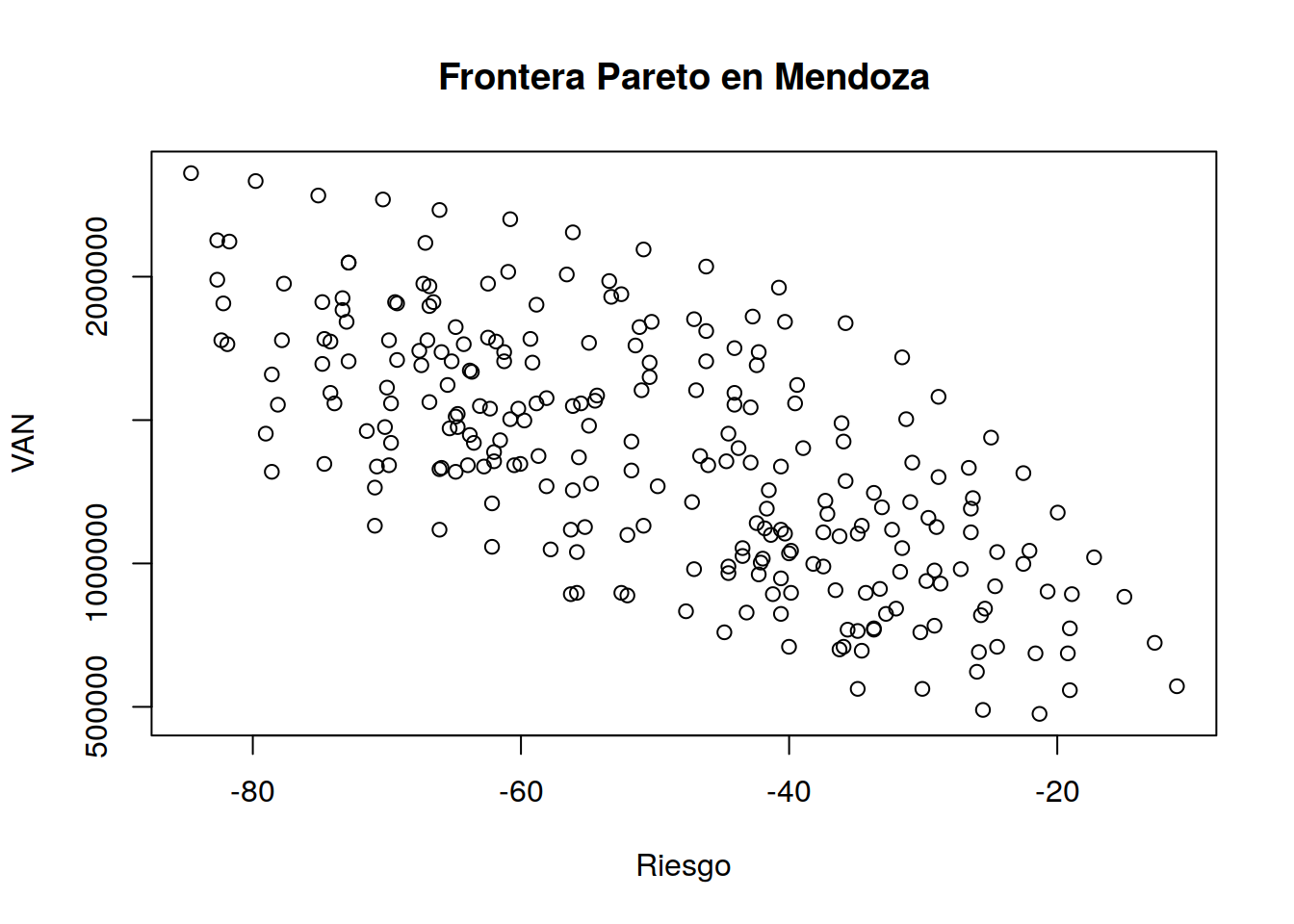
Creacion de clusters
library(cluster)
fit <- kmeans(datos, 5)
fit## K-means clustering with 5 clusters of sizes 45, 24, 60, 55, 70
##
## Cluster means:
## VAN RISK
## 1 771876.7 31.93042
## 2 2092637.9 66.17535
## 3 1100270.2 40.79803
## 4 1775219.8 61.34622
## 5 1444938.7 55.04284
##
## Clustering vector:
## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [23] 3 1 3 3 3 3 1 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1
## [45] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 1 3 3 3 3 3
## [67] 5 3 3 3 3 3 3 3 3 5 5 5 5 5 5 5 3 3 3 3 3 3
## [89] 1 1 3 3 3 3 3 3 3 3 5 5 5 5 5 5 5 5 5 5 4 5
## [111] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 3 5 3 3 5 3
## [133] 3 5 5 5 5 5 5 5 5 5 5 5 4 5 5 5 5 5 3 5 5 5
## [155] 5 5 5 5 5 3 3 3 1 5 5 5 5 5 5 4 4 4 4 4 4 4
## [177] 4 4 4 4 2 2 2 4 4 2 2 4 4 4 4 4 4 4 4 4 4 4
## [199] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
## [221] 4 2 4 2 2 2 2 4 2 4 4 2 2 2 1 1 1 3 3 5 5 5
## [243] 4 4 2 2 2 2 2 2 2 2 2 2
##
## Within cluster sum of squares by cluster:
## [1] 669483568609 375204423804 517368427229
## [4] 406220574972 671089067812
## (between_SS / total_SS = 94.1 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss"
## [4] "withinss" "tot.withinss" "betweenss"
## [7] "size" "iter" "ifault"Crear nombres
aggregate(datos,by=list(fit$cluster),FUN=mean)## Group.1 VAN RISK
## 1 1 771876.7 31.93042
## 2 2 2092637.9 66.17535
## 3 3 1100270.2 40.79803
## 4 4 1775219.8 61.34622
## 5 5 1444938.7 55.04284mi_cluster <- data.frame(datos, fit$cluster)Ver mi cluster
mi_cluster## VAN RISK fit.cluster
## 1 558095.9 19.06216 1
## 2 475519.7 21.32237 1
## 3 489282.4 25.54146 1
## 4 562683.5 30.06202 1
## 5 562683.5 34.88375 1
## 6 686547.9 19.21282 1
## 7 773711.7 19.06216 1
## 8 686547.9 21.62384 1
## 9 709485.7 24.48668 1
## 10 691135.4 25.84293 1
## 11 622321.9 25.99359 1
## 12 892988.5 18.91150 1
## 13 902163.6 20.71973 1
## 14 842525.2 25.39080 1
## 15 819587.4 25.69227 1
## 16 782886.8 29.15791 1
## 17 759949.0 30.21268 1
## 18 695723.0 34.58243 1
## 19 709485.7 35.93852 1
## 20 764536.6 34.88375 1
## 21 769124.1 33.67832 1
## 22 824174.9 32.77420 1
## 23 938864.2 29.76055 3
## 24 920513.9 24.63750 1
## 25 998502.6 22.52795 3
## 26 1044378.3 22.07582 3
## 27 1039790.7 24.48668 3
## 28 980152.3 27.19902 3
## 29 929689.1 28.70577 1
## 30 975564.8 29.15791 3
## 31 970977.2 31.71943 3
## 32 911338.8 33.22634 1
## 33 897576.1 34.28111 1
## 34 906751.2 36.54132 1
## 35 842525.2 32.02091 1
## 36 773711.7 33.67832 1
## 37 769124.1 35.63720 1
## 38 709485.7 40.00695 1
## 39 700310.6 36.23984 1
## 40 759949.0 44.82884 1
## 41 828762.5 43.17127 1
## 42 824174.9 40.60975 1
## 43 897576.1 39.85629 1
## 44 892988.5 41.21239 1
## 45 948039.3 40.60975 3
## 46 961802.0 42.26716 3
## 47 966389.6 44.52736 3
## 48 1026028.0 43.47259 3
## 49 1016852.9 41.96584 3
## 50 1044378.3 39.85629 3
## 51 998502.6 38.19873 3
## 52 989327.5 37.44543 3
## 53 1035203.2 40.00695 3
## 54 1104016.7 40.30827 3
## 55 1122367.0 41.81518 3
## 56 1053553.4 43.47259 3
## 57 1003090.2 42.11650 3
## 58 989327.5 44.52736 3
## 59 980152.3 47.08904 3
## 60 833350.1 47.69168 1
## 61 888400.9 52.06143 1
## 62 1117779.4 32.32223 3
## 63 1131542.1 34.58243 3
## 64 1094841.6 36.23984 3
## 65 1172830.2 37.14396 3
## 66 1218705.9 37.29462 3
## 67 1287519.5 35.78786 5
## 68 1246231.4 33.67832 3
## 69 1195768.1 33.07568 3
## 70 1214118.4 30.96613 3
## 71 1159067.5 29.60989 3
## 72 1126954.6 29.00725 3
## 73 1108604.3 26.44557 3
## 74 1191180.5 26.44557 3
## 75 1227881.1 26.29491 3
## 76 1333395.2 26.59623 5
## 77 1301282.2 28.85659 5
## 78 1351745.4 30.81532 5
## 79 1503135.2 31.26745 5
## 80 1489372.5 36.08918 5
## 81 1425146.6 35.93852 5
## 82 1402208.7 38.95218 5
## 83 1099429.1 41.36305 3
## 84 1108604.3 37.44543 3
## 85 1104016.7 34.88375 3
## 86 1053553.4 31.56877 3
## 87 1117779.4 40.60975 3
## 88 1140717.2 42.41782 3
## 89 897576.1 52.51357 1
## 90 892988.5 56.28052 1
## 91 1039790.7 55.82854 3
## 92 1048965.9 57.78743 3
## 93 1117779.4 56.28052 3
## 94 1126954.6 55.22575 3
## 95 1099429.1 52.06143 3
## 96 1131542.1 50.85600 3
## 97 1191180.5 41.66452 3
## 98 1255406.5 41.51371 3
## 99 1337982.8 40.60975 5
## 100 1351745.4 42.86995 5
## 101 1356333.0 44.67802 5
## 102 1374683.3 46.63691 5
## 103 1402208.7 43.77406 5
## 104 1452672.0 44.52736 5
## 105 1544423.4 42.86995 5
## 106 1553598.5 44.07538 5
## 107 1594886.6 44.07538 5
## 108 1558186.1 39.55497 5
## 109 1622412.1 39.40416 4
## 110 1604061.8 46.93838 5
## 111 1604061.8 51.00666 5
## 112 1585711.5 54.32179 5
## 113 1558186.1 55.52722 5
## 114 1576536.4 58.08875 5
## 115 1539835.8 60.19829 5
## 116 1549010.9 63.06129 5
## 117 1512310.4 64.86936 5
## 118 1471022.3 65.32150 5
## 119 1503135.2 60.80109 5
## 120 1429734.1 61.55439 5
## 121 1420559.0 63.51327 5
## 122 1356333.0 62.00652 5
## 123 1342570.3 60.49961 5
## 124 1337982.8 62.75982 5
## 125 1319632.5 64.86936 5
## 126 1333395.2 65.92414 5
## 127 1209530.8 62.15718 3
## 128 1278344.3 54.77377 5
## 129 1255406.5 56.12986 3
## 130 1269169.2 58.08875 3
## 131 1324220.0 51.76011 5
## 132 1269169.2 49.80123 3
## 133 1214118.4 47.23970 3
## 134 1342570.3 46.03427 5
## 135 1425146.6 51.76011 5
## 136 1480197.4 54.92443 5
## 137 1567361.2 54.47245 5
## 138 1549010.9 56.12986 5
## 139 1558186.1 58.84220 5
## 140 1498547.7 59.74631 5
## 141 1539835.8 62.30784 5
## 142 1521485.5 64.71870 5
## 143 1562773.6 66.82825 5
## 144 1558186.1 69.69125 5
## 145 1613236.9 69.99257 4
## 146 1475609.8 70.14323 5
## 147 1420559.0 69.69125 5
## 148 1461847.1 71.49947 5
## 149 1342570.3 69.84191 5
## 150 1337982.8 70.74602 5
## 151 1264581.6 70.89668 3
## 152 1328807.6 66.07495 5
## 153 1342570.3 63.96541 5
## 154 1388446.0 62.00652 5
## 155 1347157.9 60.04763 5
## 156 1448084.4 63.81459 5
## 157 1475609.8 64.71870 5
## 158 1370095.7 55.67788 5
## 159 1374683.3 58.69154 5
## 160 1131542.1 70.89668 3
## 161 1117779.4 66.07495 3
## 162 1058141.0 62.15718 3
## 163 897576.1 55.82854 1
## 164 1319632.5 78.58141 5
## 165 1452672.0 79.03354 5
## 166 1347157.9 74.66379 5
## 167 1558186.1 73.91034 5
## 168 1594886.6 74.21166 5
## 169 1553598.5 78.12943 5
## 170 1704988.3 72.85557 4
## 171 1695813.2 74.81445 4
## 172 1773801.9 74.21166 4
## 173 1778389.4 77.82811 4
## 174 1659112.6 78.58141 4
## 175 1764626.7 81.89639 4
## 176 1782977.0 74.66379 4
## 177 1842615.4 73.00623 4
## 178 1883903.5 73.30755 4
## 179 1925191.6 73.30755 4
## 180 1911428.9 74.81445 4
## 181 1975654.9 77.67745 2
## 182 2127044.7 82.64984 2
## 183 1989417.6 82.64984 2
## 184 1906841.4 82.19786 4
## 185 1778389.4 82.34852 4
## 186 2049056.0 72.85557 2
## 187 1966479.8 66.82825 2
## 188 1906841.4 69.23927 4
## 189 1911428.9 66.52693 4
## 190 1824265.1 64.86936 4
## 191 1778389.4 66.97891 4
## 192 1778389.4 69.84191 4
## 193 1709575.9 69.23927 4
## 194 1741688.9 67.58170 4
## 195 1737101.3 65.92414 4
## 196 1691225.6 67.43104 4
## 197 1704988.3 65.17084 4
## 198 1622412.1 65.47216 4
## 199 1672875.3 63.81459 4
## 200 1764626.7 64.26672 4
## 201 1787564.6 62.45850 4
## 202 1737101.3 61.25307 4
## 203 1704988.3 61.25307 4
## 204 1668287.8 63.66393 4
## 205 1700400.7 59.14352 4
## 206 1773801.9 61.85586 4
## 207 1782977.0 59.29418 4
## 208 1769214.3 54.92443 4
## 209 1842615.4 50.25336 4
## 210 1824265.1 51.15747 4
## 211 1760039.1 51.45879 4
## 212 1700400.7 50.40402 4
## 213 1649937.5 50.40402 4
## 214 1704988.3 46.18493 4
## 215 1750864.0 44.07538 4
## 216 1737101.3 42.26716 4
## 217 1691225.6 42.41782 4
## 218 1842615.4 40.30827 4
## 219 1860965.7 42.71929 4
## 220 1851790.5 47.08904 4
## 221 1810502.4 46.18493 4
## 222 1938954.4 52.51357 2
## 223 1929779.2 53.26702 4
## 224 1984830.1 53.41768 2
## 225 2007767.9 56.58200 2
## 226 2016943.0 60.95175 2
## 227 1975654.9 62.45850 2
## 228 1902253.8 58.84220 4
## 229 1975654.9 67.28038 2
## 230 1897666.2 66.82825 4
## 231 1911428.9 69.38993 4
## 232 2117869.6 67.12972 2
## 233 2049056.0 72.85557 2
## 234 2122457.1 81.74573 2
## 235 571858.6 11.07611 1
## 236 723248.4 12.73352 1
## 237 883813.4 14.99373 1
## 238 1021440.4 17.25409 3
## 239 1177417.8 19.96627 3
## 240 1315044.9 22.52795 5
## 241 1438909.3 24.93882 5
## 242 1581123.9 28.85659 5
## 243 1718751.0 31.56877 4
## 244 1838027.8 35.78786 4
## 245 1961892.2 40.76041 2
## 246 2035293.3 46.18493 2
## 247 2094931.7 50.85600 2
## 248 2154570.1 56.12986 2
## 249 2200445.8 60.80109 2
## 250 2232558.8 66.07495 2
## 251 2269259.4 70.29404 2
## 252 2283022.1 75.11577 2
## 253 2333485.3 79.78684 2
## 254 2361010.8 84.60873 2Ploteo de Clusters con PCA
clusplot(mi_cluster,mi_cluster$fit.cluster)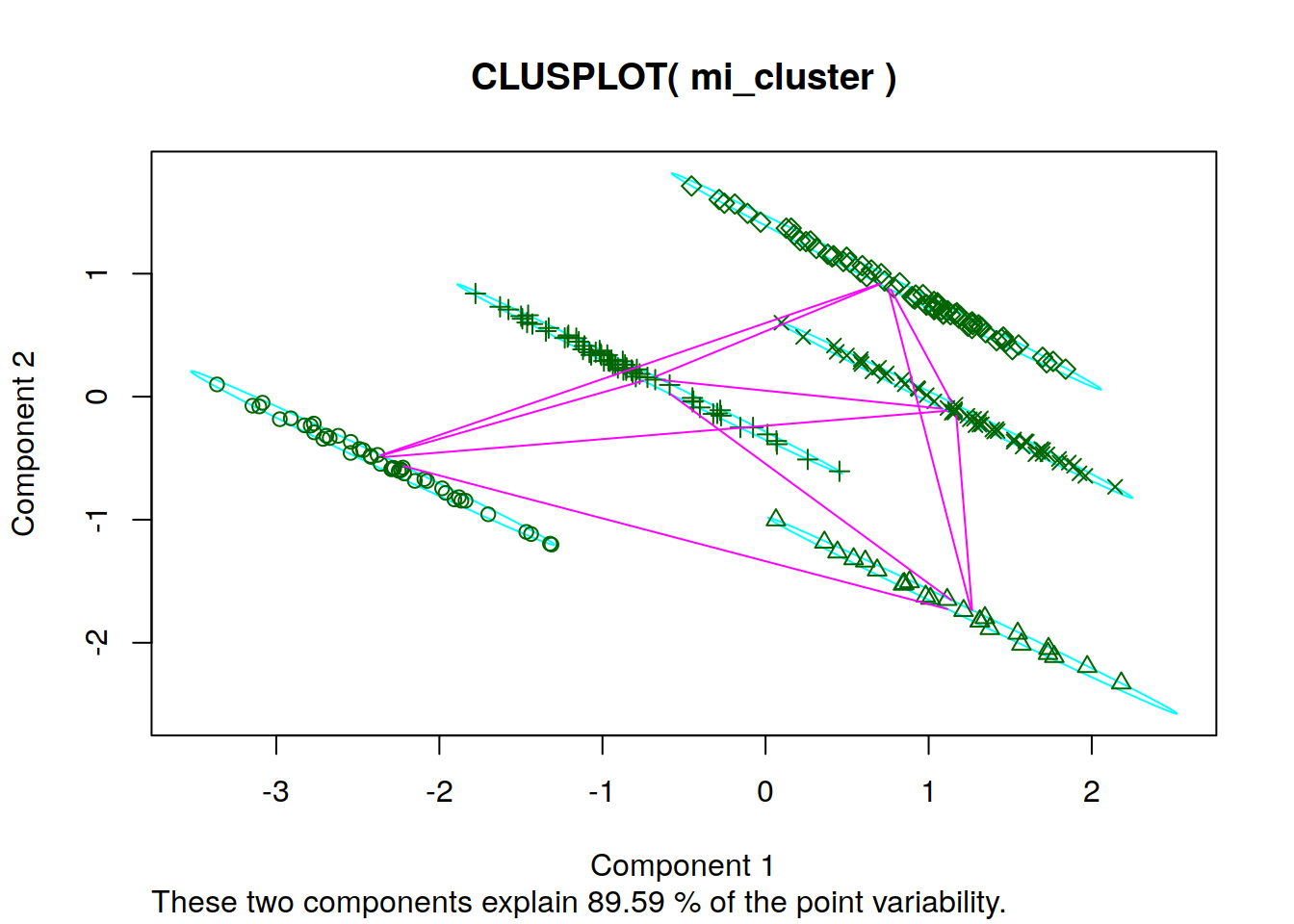
Figura de Familias
plot(mi_cluster$RISK , mi_cluster$VAN , col=mi_cluster$fit.cluster)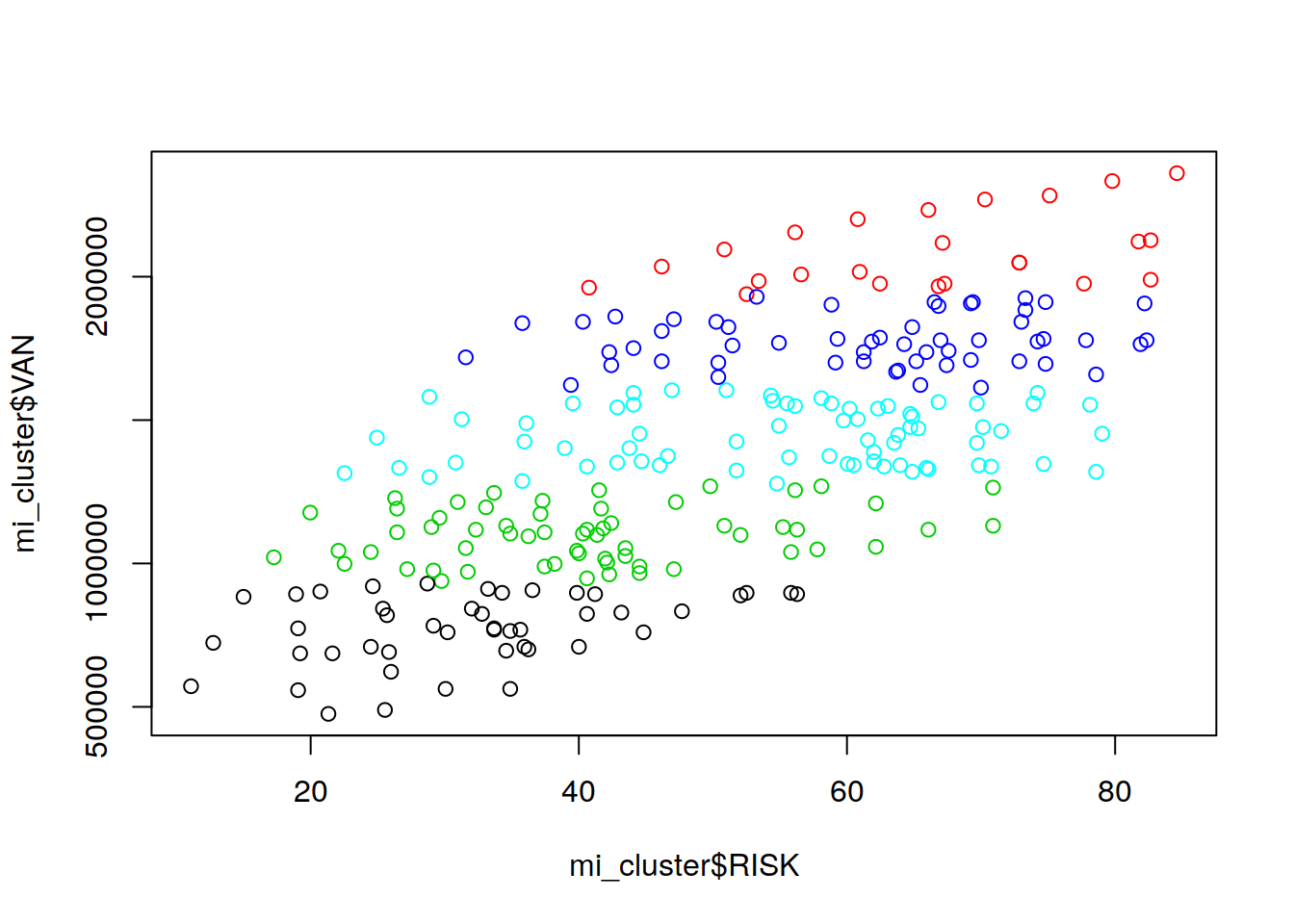
Entrenamiento KNN
train <- mi_cluster
cl <- factor(mi_cluster$fit.cluster, levels = c("1", "2","3","4","5"),labels = c("Prost Penalist Casino","Bank Cred_pers Tel_Cel Bebidas", "Manufactura Metal_Mec Servicios Seguros,Bodegas","MOA Restaurant Emprendimientos BT","Transporte Pasajeros Comercio Ropa, Perecederos"))Caso de estudio
Empresa del Rubro alimentacion (3) VAN 500.000 * RISK 62,23%
mi_caso <- cbind (5000000,62.23,3 )
#mi_caso <- train[5, ]
mi_caso## [,1] [,2] [,3]
## [1,] 5e+06 62.23 3Busco 5 vecinos más próximos
library(class)
knn(train, mi_caso, k=5, cl, prob=TRUE)## [1] Bank Cred_pers Tel_Cel Bebidas
## attr(,"prob")
## [1] 1
## 5 Levels: Prost Penalist Casino ...10.3 Riesgo y Estacionalidad
10.4 ARIMA S-ARIMA
10.4.1 Introducción
ARIMA es una técnica básica para el pronóstico de series de tiempo complejas , si son series estacionales se usa S-ARIMA (Seasonal). Este artículo provee una descripción paso a paso para hacer el ajuste y parametrización la biblioteca arima usando r. Arima es modelo muy popular para simulado y pronóstico de escenarios para empresas de base tecnológica, es flexible ideal para trabajar modelos con variaciones estacionales a partir de información histórica de datos que no son relativos al producto innovador, pero que sí son complementarios o sustitutos. Especialmente para hacer predicciones en los escenarios futuros. Este modelo básico de pronóstico y sus técnicas asociadas pueden ser usados como base para modelos más complejos, como los casos en los que la empresas innovadoras lanzan acciones o fondos de crowdfunding. En este caso de estudio nosotros haremos sobre un ejemplo que examina una serie de tiempo de la demanda de bicicletas en una zona urbana (bicicletas públicas de alquiler) que están relacionadas con el lanzamiento al mercado de una app para proveer información a los dueños de negocios sobre recorridos frecuentes de potenciales clientes que pasan por sus locales. Trataremos de ajustar los parámetros de arima para que se adecuén a este modelo tomando los datos del pasado y proyectando los datos que tenemos en la actualidad (entrenamiento de modelo) para que se ajusten más tarde a la demanda real en el futuro. También generaremos una lista de revisión de los pasos a seguir para ajustar otros tipos de modelos.
ARIMA por sus siglas en inglés , acrónimo del inglés autoregressive integrated moving average , o Modelo autorregresivo integrado de media móvil es muy utilizado en estadística y econometría, en particular en series temporales, un modelo autorregresivo integrado de promedio móvil o simplemente un sistema que se comporta como ARIMA es un modelo estadístico que utiliza variaciones y regresiones de datos estadísticos con el fin de encontrar patrones para una predicción hacia el futuro. Se trata de un modelo dinámico de series temporales, es decir, las estimaciones futuras vienen explicadas por los datos del pasado y no por variables independientes. Fue desarrollado a finales de los sesenta del siglo XX. Box y Jenkins (1976)
10.4.2 Business as Usual
El modelo ARIMA necesita identificar los coeficientes y número de regresiones que se utilizarán. Este modelo es muy sensible a la precisión con que se determinen sus coeficientes.
Se suele expresar como ARIMA(p,d,q) donde los parámetros p, d y q son números enteros no negativos que indican el orden de las distintas componentes del modelo — respectivamente, las componentes autorregresiva, integrada y de media móvil. Cuando alguno de los tres parámetros es cero, es común omitir las letras correspondientes del acrónimo — AR para la componente autorregresiva, I para la integrada y MA para la media móvil. Por ejemplo, ARIMA(0,1,0) se puede expresar como I(1) y ARIMA(0,0,1) como MA(1).
El modelo ARIMA puede generalizarse aún más para considerar el efecto de la estacionalidad. En ese caso, se habla de un modelo SARIMA (seasonal autoregressive integrated moving average).
El modelo ARIMA (p,d,q) se puede representar como:
\[ Y_t= -(\Delta^{d} Y_{t}- Y{t}) + \phi_{0} +\sum _{i=1}^{p}\phi _{i} \Delta ^{d}Y_{t-i} -\sum _{i=1}^{q}\theta _{i}\varepsilon _{t-i}+\varepsilon _{t} \displaystyle \]
en donde \(d\) corresponde a las d diferencias que son necesarias para convertir la serie original en estacionaria, \(\phi_{1},\dot,\dot,\dot,\phi{p}\) son los parámetros pertenecientes a la parte "autorregresiva" del modelo, \({\displaystyle \theta _{1},\ldots ,\theta _{q}}{\displaystyle \theta _{1},\ldots ,\theta _{q}}\) los parámetros pertenecientes a la parte "medias móviles" del modelo.
\(\phi_{0}\) es una constante para cada modelo y \(\varepsilon _{t}\) es el término de error (llamado también innovación o perturbación estocástica esta última asociada más para modelos econométricos uniecuacionales o multiecuacionales).
Se debe tomar en cuenta que:
\[{\displaystyle \Delta Y_{t}=Y_{t}-Y_{t-1}}\]
10.5 Caso de estudio
Comenzaremos modelando los datos de una serie temporal. Usando R, convertiremos los datos disponibles en formato de datos de serie temporal. Para hacer esto, ejecutaremos el siguiente comando:
RawData=scan('https://themys.sid.uncu.edu.ar/~rpalma/R-cran/Routers.txt')
plot(RawData)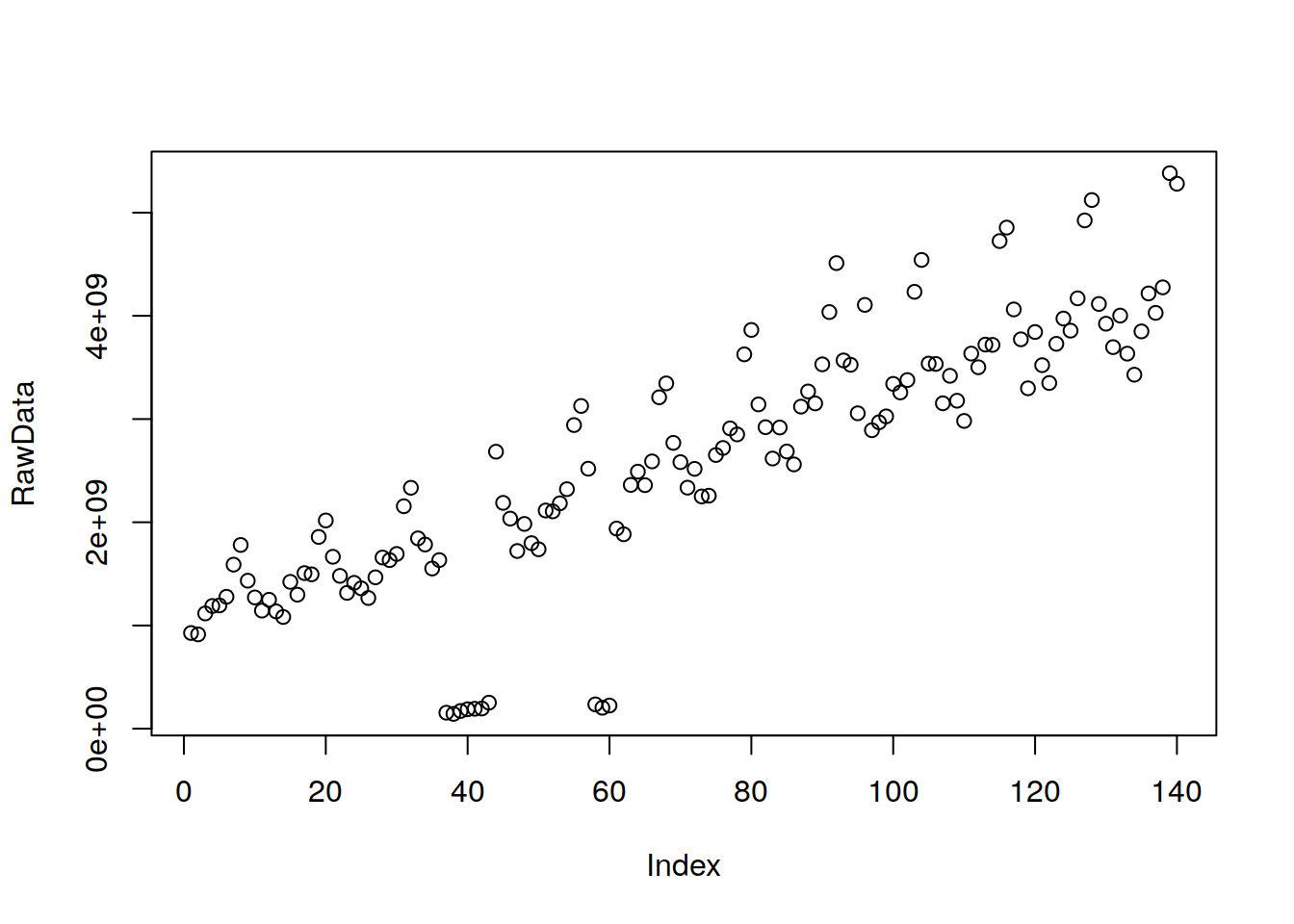
Venta de routers de uso hogareños en América Latina
tsData = ts(RawData, start = c(2006,1), frequency = 12)
print(tsData)## Jan Feb Mar Apr
## 2006 927180000 913800000 1116430000 1188880000
## 2007 1136610000 1082240000 1422560000 1298350000
## 2008 1359510000 1266150000 1466470000 1658220000
## 2009 154844000 143552000 171573000 188322000
## 2010 1797590000 1738210000 2113870000 2105510000
## 2011 1939160000 1883750000 2361870000 2490370000
## 2012 2250100000 2257420000 2651590000 2719860000
## 2013 2685780000 2560630000 3120410000 3267410000
## 2014 2891860000 2968810000 3025890000 3340910000
## 2015 3177600000 2981880000 3634290000 3502030000
## 2016 3522000000 3349380000 3728910000 3973880000
## 2017 3633670000 3429790000 3849360000 4217180000
## May Jun Jul Aug
## 2006 1194320000 1277960000 1589430000 1780130000
## 2007 1507350000 1495540000 1857920000 2017580000
## 2008 1633650000 1692940000 2155380000 2334270000
## 2009 192756000 195296000 252288000 2683790000
## 2010 2183710000 2320570000 2941730000 3127000000
## 2011 2359570000 2589800000 3210850000 3345620000
## 2012 2909530000 2851080000 3626870000 3863470000
## 2013 3151570000 3530160000 4036620000 4510980000
## 2014 3257900000 3377820000 4232970000 4541720000
## 2015 3721490000 3718770000 4724580000 4855170000
## 2016 3856570000 4169610000 4924800000 5122090000
## 2017 4028770000 4276150000 5382540000 5280070000
## Sep Oct Nov Dec
## 2006 1433850000 1271790000 1144030000 1249000000
## 2007 1665650000 1480480000 1315810000 1413150000
## 2008 1844020000 1784320000 1551790000 1633550000
## 2009 2188100000 2035450000 1721480000 1983810000
## 2010 2518910000 235560000 202876000 224383000
## 2011 2769320000 2582690000 2335320000 2517550000
## 2012 3142050000 2921240000 2617400000 2918100000
## 2013 3568110000 3525660000 3055800000 4106140000
## 2014 3537270000 3534130000 3152720000 3419020000
## 2015 4062230000 3772620000 3297940000 3843500000
## 2016 4115140000 3923800000 3696710000 4002430000
## 2017plot(tsData)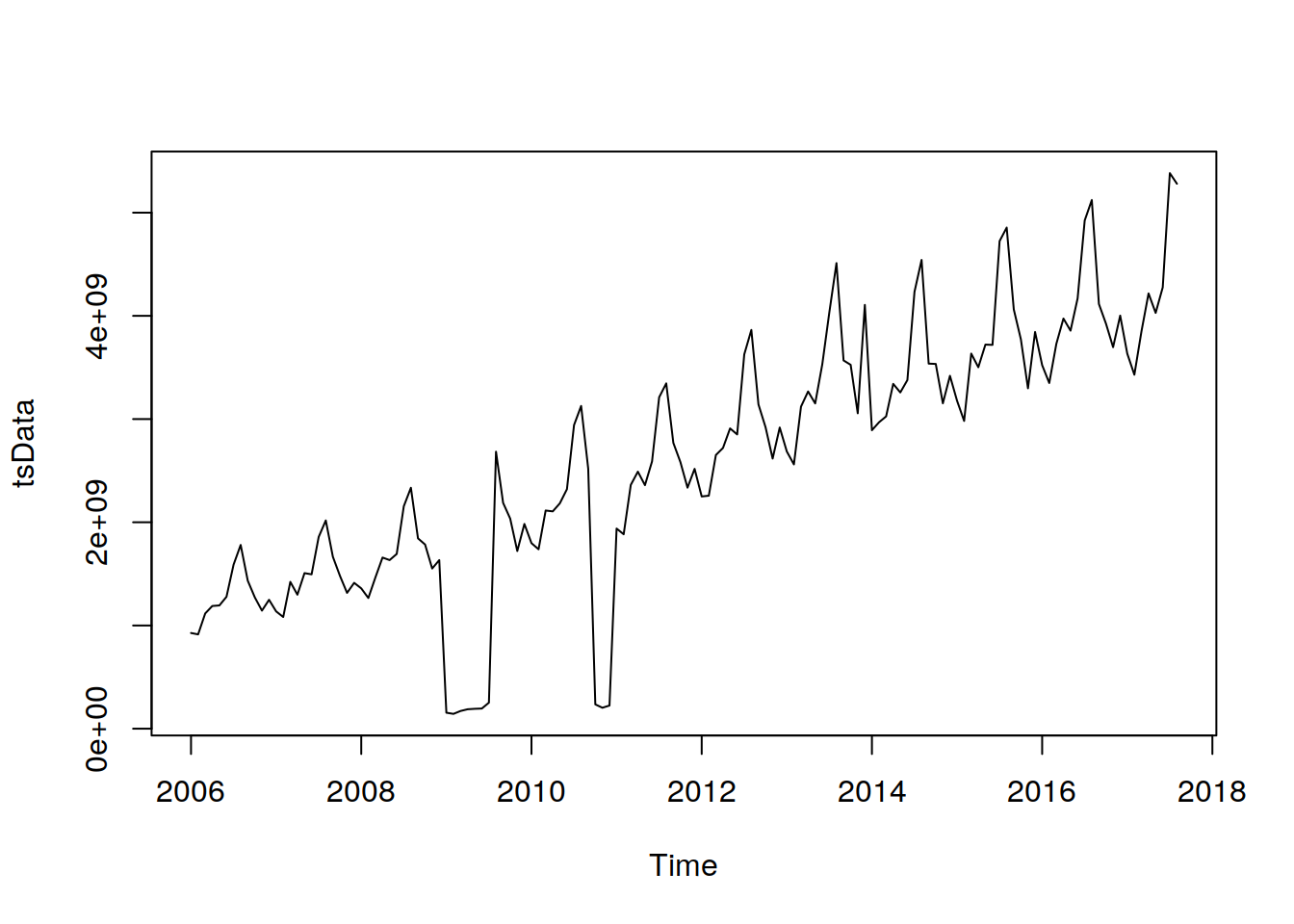
Podemos deducir del gráfico en sí mismo que los puntos de datos siguen un patrón de subidas y caídas en una tendencia ascendente. Ahora necesitamos hacer un análisis para averiguar la no estacionariedad exacta y la estacionalidad en los datos.
10.5.1 Pre-Análisis Exploratorio de Datos (PAED)}
Antes de realizar cualquiera de estos pasos en los datos, debemos comprender los tres componentes de los datos de una serie temporal:
En R podemos averiguar estos componentes de la serie temporal con los siguientes comandos:
componentes.ts = decompose(tsData)
plot(componentes.ts)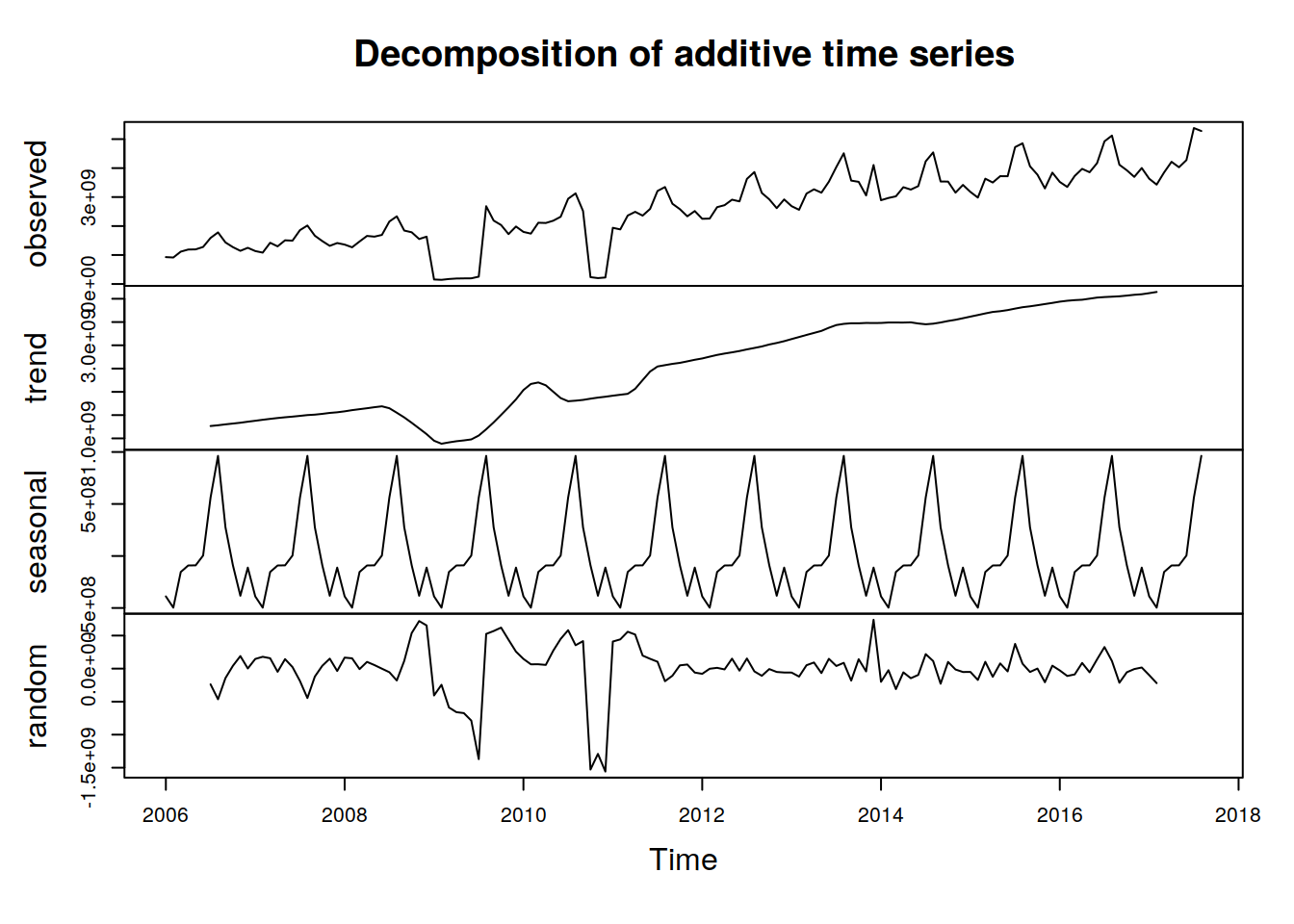
A continuación, debemos eliminar la parte no estacionaria de ARIMA. Para facilitar el análisis aquí, también eliminaremos la parte estacional de los datos. La parte estacional puede eliminarse del análisis y agregarse más tarde, o puede tratarse en el propio modelo ARIMA.
Para conseguir estacionariedad:
diferencia los datos – calcula las diferencias entre observaciones consecutivas
aplica el logaritmo o raíz cuadrada a los datos de la serie para estabilizar la varianza no constante
Si los datos contienen una tendencia, ajusta algún tipo de curva a los datos y luego modela los residuales de ese ajuste. Prueba de raíz unitaria: esta prueba se usa para descubrir la primera diferencia o regresión que se debe usar en los datos de tendencias para hacerla estacionaria. En la prueba Kwiatkowski-Phillips-Schmidt-Shin (KPSS), los valores pequeños de p sugieren que se requiera una diferenciación.
El codigo R para la prueba de raíz unitaria:
#install.packages("fUnitRoots")
library("fUnitRoots")## Loading required package: timeDate## Loading required package: methods## Loading required package: timeSeries##
## Attaching package: 'timeSeries'## The following object is masked from 'package:psych':
##
## outlier## Loading required package: fBasics##
## Attaching package: 'fBasics'## The following object is masked from 'package:car':
##
## densityPlot## The following object is masked from 'package:psych':
##
## trurkpssTest(tsData, type = c("tau"), lags = c("short"),use.lag = NULL, doplot = TRUE)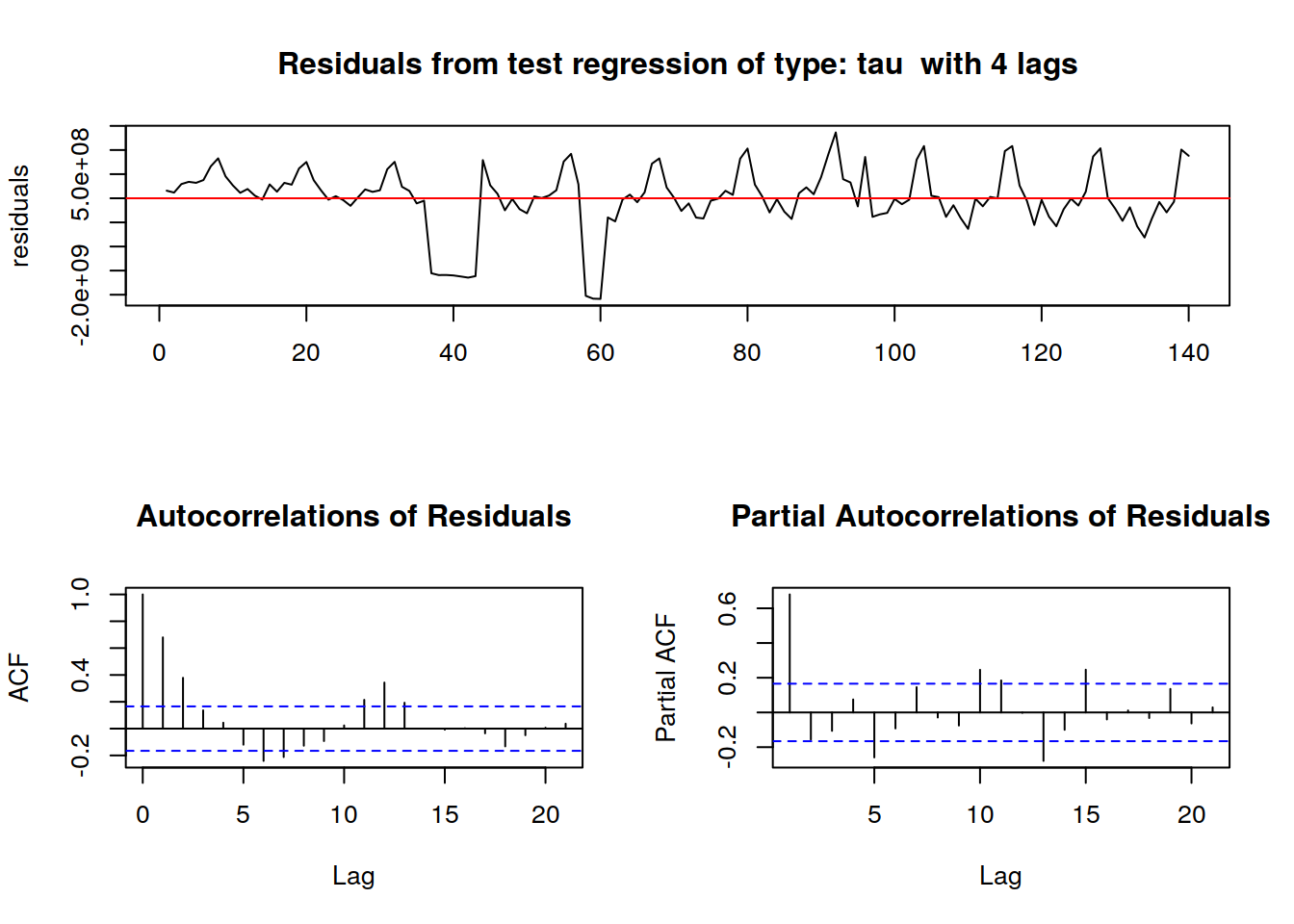
##
## Title:
## KPSS Unit Root Test
##
## Test Results:
## NA
##
## Description:
## Thu Nov 5 13:25:30 2020 by user:Después eliminamos la no estacionariedad: (tendencia lineal creciente)
tsstationary = diff(tsData, differences=1)
plot(tsstationary)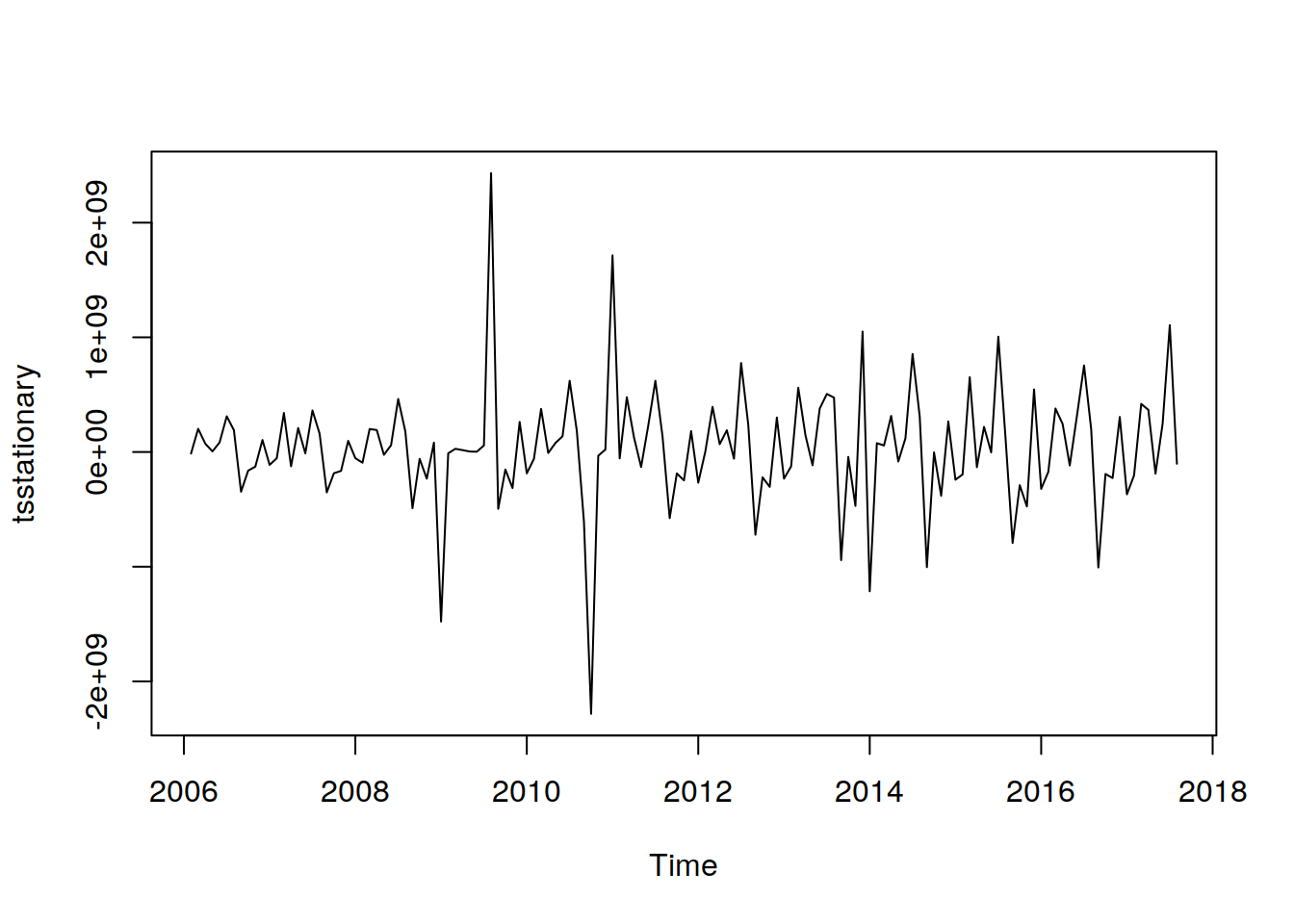
Hay diversos gráficos y funciones que nos pueden ayudar a detectar la estacionalidad:
Codigo R para calcular la autocorrelación:
acf(tsData,lag.max=140)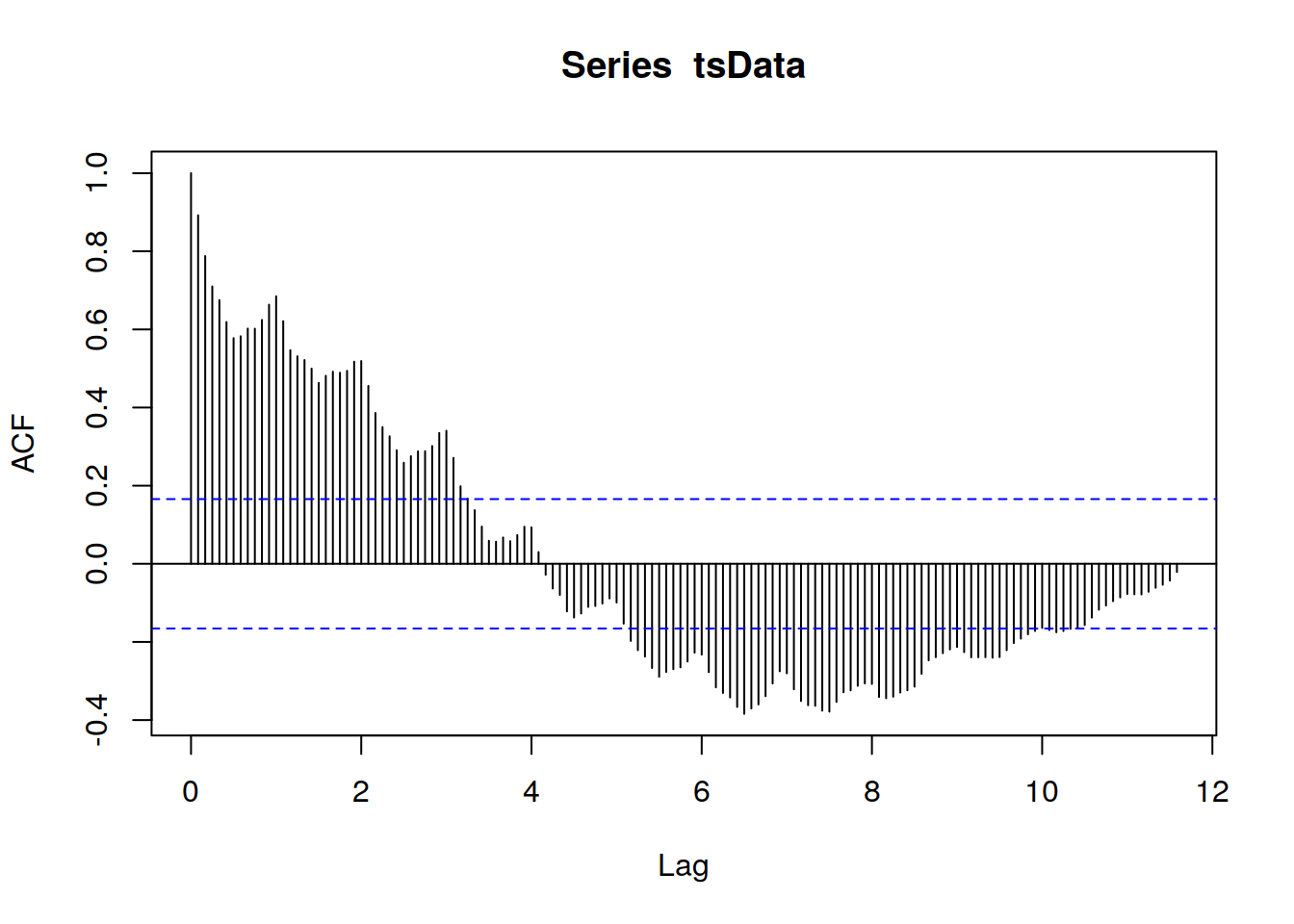
La función de autocorrelación proporciona la autocorrelación en todos los retrasos posibles. La autocorrelación en el retraso 0 se incluye por defecto, lo que siempre toma el valor 1, ya que representa la correlación entre los datos y ellos mismos. Como podemos observar en el gráfico anterior, la autocorrelación continúa disminuyendo a medida que aumenta el retraso, lo que confirma que no existe una asociación lineal entre las observaciones separadas por retrasos mayores.
timeseriesseasonallyadjusted <- tsData-componentes.ts$seasonal
tsstationary <- diff(timeseriesseasonallyadjusted, differences=1)Para eliminar la estacionalidad de los datos, restamos el componente estacional de la serie original(media cero) y luego lo diferenciamos para que sea estacionario ( varianza constante e independiente).
Después de eliminar la estacionalidad y hacer que los datos sean estacionarios, se verá así:
plot(tsstationary)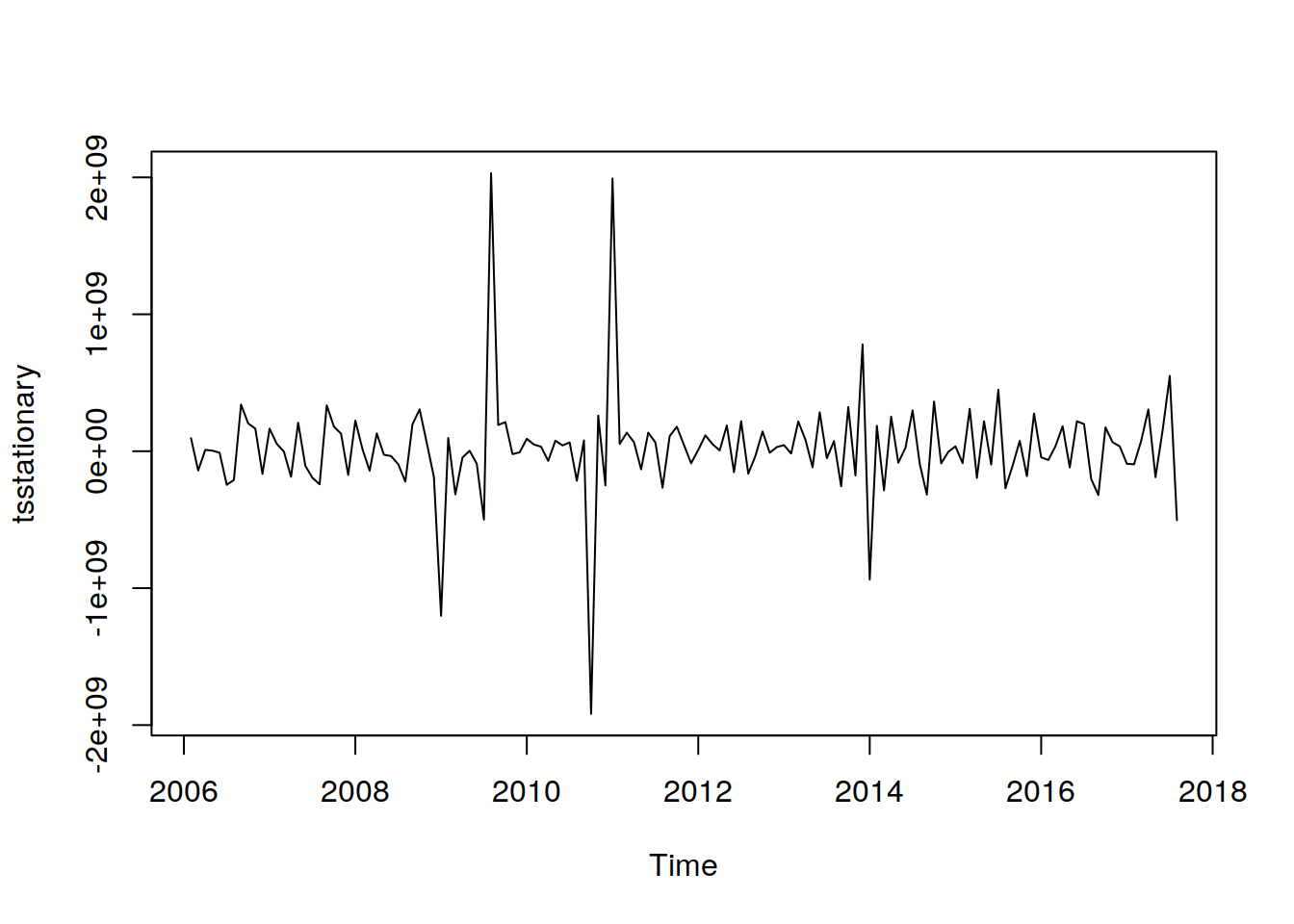
El suavizado se hace generalmente para ayudarnos a ver mejor los patrones, las tendencias en las series temporales. Generalmente alisa las irregularidades para ver una señal más clara. Para datos estacionales, podríamos suavizar la estacionalidad para que podamos identificar la tendencia. El suavizado no nos proporciona un modelo, pero puede ser un buen primer paso para describir varios componentes de la serie.
Para suavizar las series de tiempo:
10.6 Ajuste del modelo
Una vez que tenemos los datos listos y han satisfecho todas las suposiciones del modelo, para determinar el orden del modelo que se ajustará a los datos, necesitamos tres variables: p, d y q que son enteros positivos que se refieren al orden de las partes medias autorregresivas, integradas y móviles del modelo, respectivamente.
Para identificar que valores de p y q serán apropiados, necesitamos ejecutar las funciones acf() y pacf()
en el retardo k-esimo es la función de autocorrelación que describe la correlación entre todos los puntos de datos que están exactamente k pasos antes, después de tener en cuenta su correlación con los datos entre esos k pasos. Ayuda a identificar el número de coeficientes de autorregresión (AR) (valor p) en un modelo .
El código R para ejecutar los comandos :
acf(tsstationary, lag.max=140)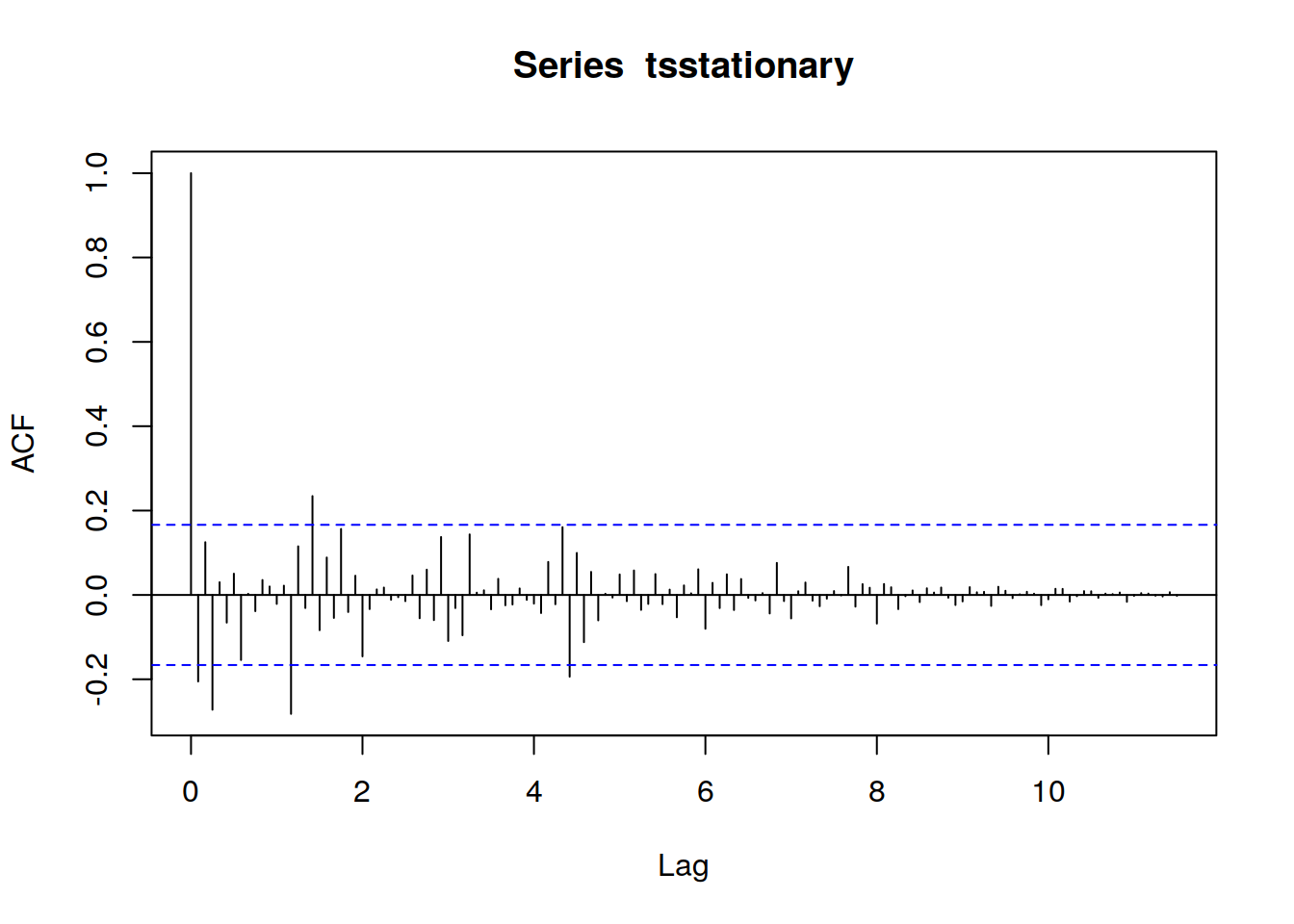
pacf(tsstationary, lag.max=140)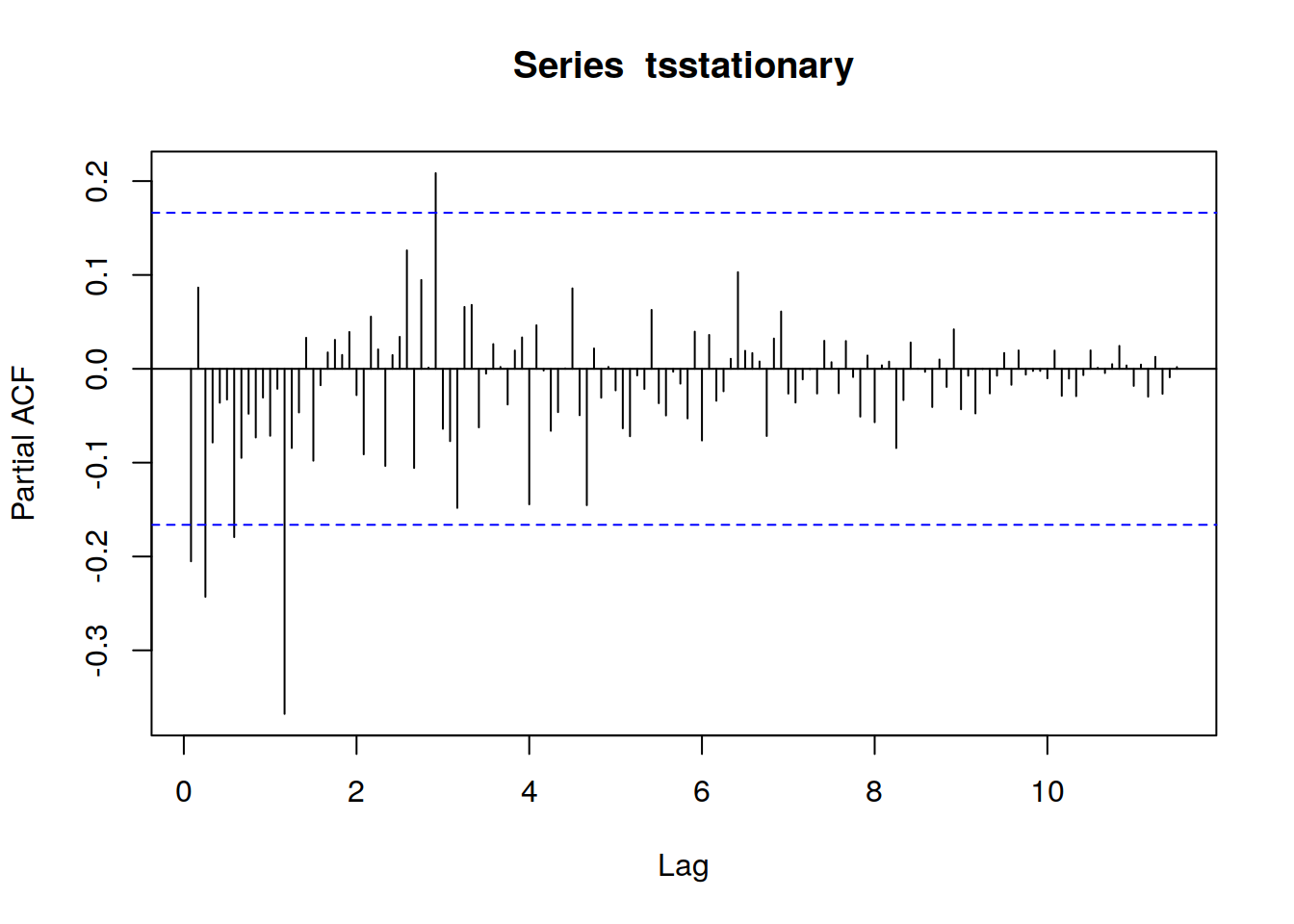
La forma de acf () para definir valores de p y q es mirar los gráficos y repasando la tabla podemos determinar qué tipo de modelo seleccionar y cuáles serán los valores de p, d y q.
library(kableExtra)library(kableExtra)
t <- c(
"Forma" ,
"Modelo",
"Serie exponencial decayendo a 0 " ,
"Modelo Auto Regresivo (AR). Función pacf () que se
utilizará para identificar el orden del modelo",
"Picos alternativos positivos y negativos, decayendo a 0",
"Modelo Auto Regresivo (AR). Función pacf () que se
utilizará para identificar el orden del modelo",
"Uno o más picos en serie, resto todos son 0" ,
"Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 ",
"Después de algunos retrasos en general la serie va decayendo.",
"Modelo mezclado AR & MA",
"La serie total es 0 o casi 0",
"Datos aleatorios ",
"Valores medios a intervalos fijos",
"Necesitamos incluir el término AR de estacionalidad",
"Picos visibles que no decaen a 0",
"Series no son estacionarias"
)
Tt <- matrix(t,8,2,byrow = TRUE)kbl(Tt)| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
kbl(Tt, booktabs = T, linesep = "") %>%
kable_styling(latex_options = "striped", stripe_index = c(1,2, 5:6))| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
10.6.1 Tabla con caption
kbl(Tt, caption = "¿Qué paramétrica usar?", booktabs = T) %>%
kable_styling(latex_options = c("striped", "hold_position"))| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
10.6.2 Tabla escalada
kbl(rbind(Tt,Tt,Tt), booktabs = T) %>%
kable_styling(latex_options = c("striped", "scale_down")) %>%
kable_styling(font_size = 7)| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
10.7 Tabla a lo ancho
kbl(Tt, booktabs = T) %>%
kable_styling(full_width = T) %>%
column_spec(1, width = "8cm")| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
10.8 Tablas centradas
kbl(Tt, booktabs = T) %>%
kable_styling(position = "center")| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
Ttt <- data.frame(Tt)
kbl(Ttt, booktabs = T) %>%
kable_styling(full_width = F) %>%
column_spec(1, bold = T, color = "red") %>%
column_spec(2, width = "30em")| X1 | X2 |
|---|---|
| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
fitARIMA <- arima(tsData, order=c(1,1,1),seasonal =list(order = c(1,0,0), period = 12),method="ML")
#install.packages("lmtest")
library(lmtest)## Loading required package: zoo##
## Attaching package: 'zoo'## The following object is masked from 'package:timeSeries':
##
## time<-## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numericcoeftest(fitARIMA)##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 -0.795254 0.108606 -7.3224 2.436e-13 ***
## ma1 0.648118 0.129662 4.9985 5.777e-07 ***
## sar1 0.484253 0.074262 6.5209 6.991e-11 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1fitARIMA <- arima(tsData, order=c(1,1,1), seasonal =list(order = c(1,0,0), period = 12),method="ML")El proceso de ajuste es un proceso recursivo y necesitamos ejecutar esta función arima () con diferentes valores (p, d, q) para encontrar el modelo más optimizado y eficiente.
La salida de fitarima () incluye los coeficientes ajustados y el error estándar para cada coeficiente. Observando los coeficientes podemos excluir los insignificantes. Podemos usar una función confint () para este propósito. Podemos usar una función confint () para este propósito.
confint(fitARIMA)## 2.5 % 97.5 %
## ar1 -1.0081178 -0.5823911
## ma1 0.3939846 0.9022509
## sar1 0.3387016 0.629803810.8.1 Elección del mejor modelo
R utiliza la estimación de máxima verosimilitud (MLE) para estimar el modelo ARIMA. Intenta maximizar la probabilidad logarítmica para valores dados de p, d y q al encontrar estimaciones de parámetros para maximizar la probabilidad de obtener los datos que hemos observado. Averigüa el Criterio de Información de Akaike (AIC) para un conjunto de modelos e investigarlos modelos con los valores AIC más bajos. Prueba el criterio de información bayesiano (BIC) de Schwarz e investiga los modelos con los valores BIC más bajos. Al estimar los parámetros del modelo utilizando la estimación de máxima verosimilitud, es posible aumentar la probabilidad agregando parámetros adicionales, lo que puede resultar en un ajuste excesivo. El BIC resuelve este problema introduciendo un término de penalización para el número de parámetros en el modelo. Junto con AIC y BIC, también debemos observar de cerca los valores de los coeficientes y debemos decidir si incluir ese componente o no de acuerdo con su nivel de significación.
10.8.2 Medidas de diagnostico
Deben observarse los coeficientes de autocorrelación muestral de los residuos y comprobar que ninguno
de ellos supera el valor de las bandas de significatividad al \(5\% (±1,96(1/T ))^{1/2}\). El valor T es una aproximación de la varianza asintótica pero resulta sólo adecuada para valores grandes de «j». Se
aconseja,por tanto, utilizar distinta amplitud de bandas como por ejemplo \(±(1/T )^{1/2}\) para los términos más cercanos a cero.Intenta averiguar el patrón en los residuos del modelo elegido trazando el ACF de los residuos y haciendo una prueba de portmanteau. Necesitamos probar modelos modificados si la gráfica no parece un ruido blanco. Una vez que los residuos parezcan ruido blanco, calcularemos los pronósticos.
10.8.3 Prueba de Box-Ljung
Es una prueba para comprobar si una serie de observaciones en un período de tiempo especifico son aleatorias o independientes en todos los retardos hasta el especificado. En lugar de probar la aleatoriedad en cada retardo distinto, prueba la aleatoriedad «general» basada en un número de retardos y, por lo tanto, es una prueba de comparación. Se aplica a los residuos de un modelo ARIMA ajustado, no a la serie original, y en tales aplicaciones, la hipótesis que se está probando realmente es que los residuos del modelo ARIMA no tienen autocorrelación. Si los retardos no son independientes, un retardo puede estar relacionado con otros retardos k unidades de tiempo después por lo que la autocorrelacion puede reducir la exactitud de un modelo predictivo basado en el tiempo y conducir a una interpretación errónea de los datos. El código R para obtener los resultados de la prueba Box:
#install.packages("FitAR")
library(FitAR)## Loading required package: lattice##
## Attaching package: 'lattice'## The following object is masked from 'package:boot':
##
## melanoma## Loading required package: leaps## Loading required package: ltsa## Loading required package: bestglm##
## Attaching package: 'FitAR'## The following object is masked from 'package:car':
##
## Bootacf(fitARIMA$residuals,lag.max=140)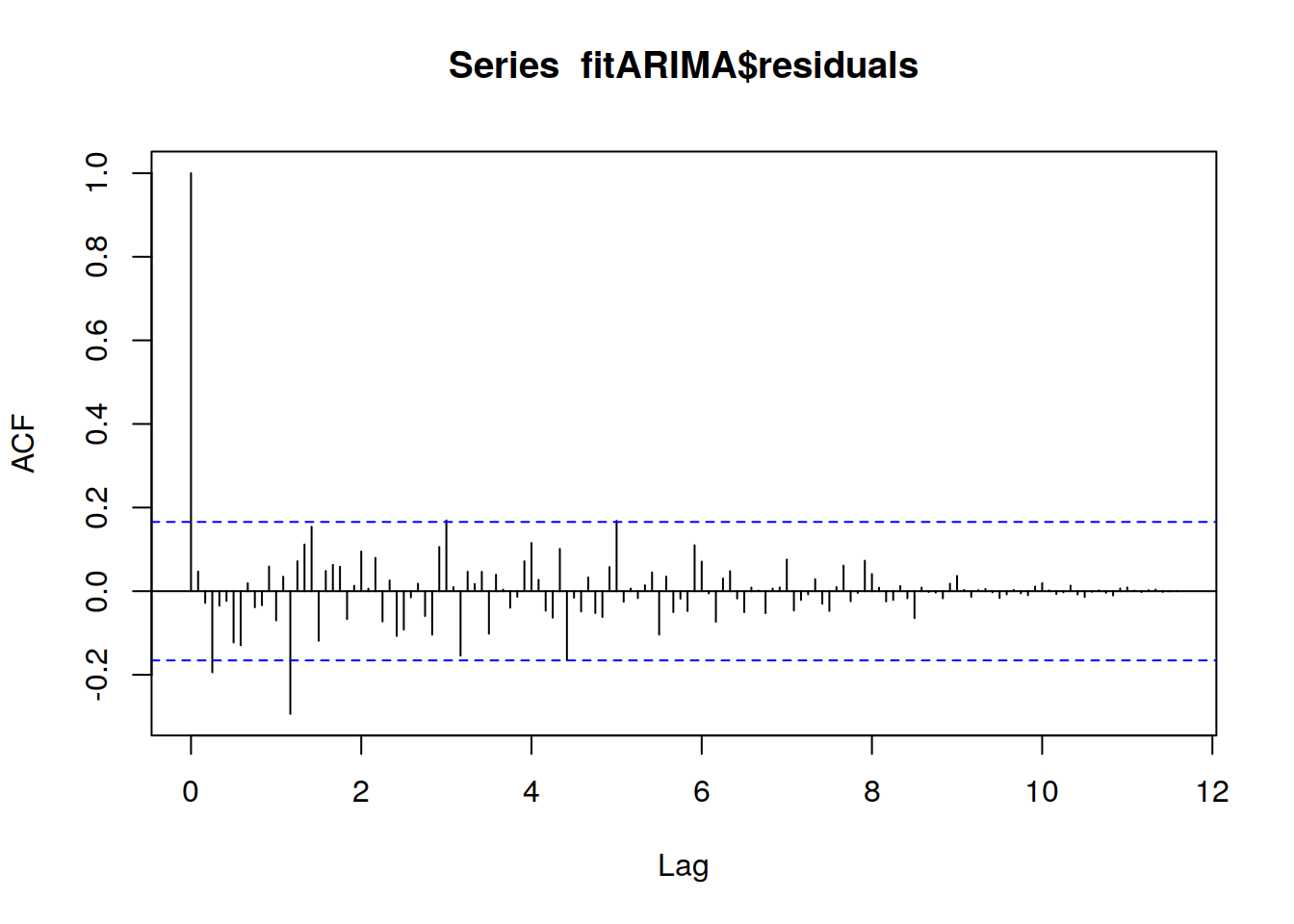
boxresult=LjungBoxTest (fitARIMA$residuals,k=2,StartLag=1)
plot(boxresult[,3],main= "Ljung-Box Q Test", ylab= "P-values", xlab= "Lag")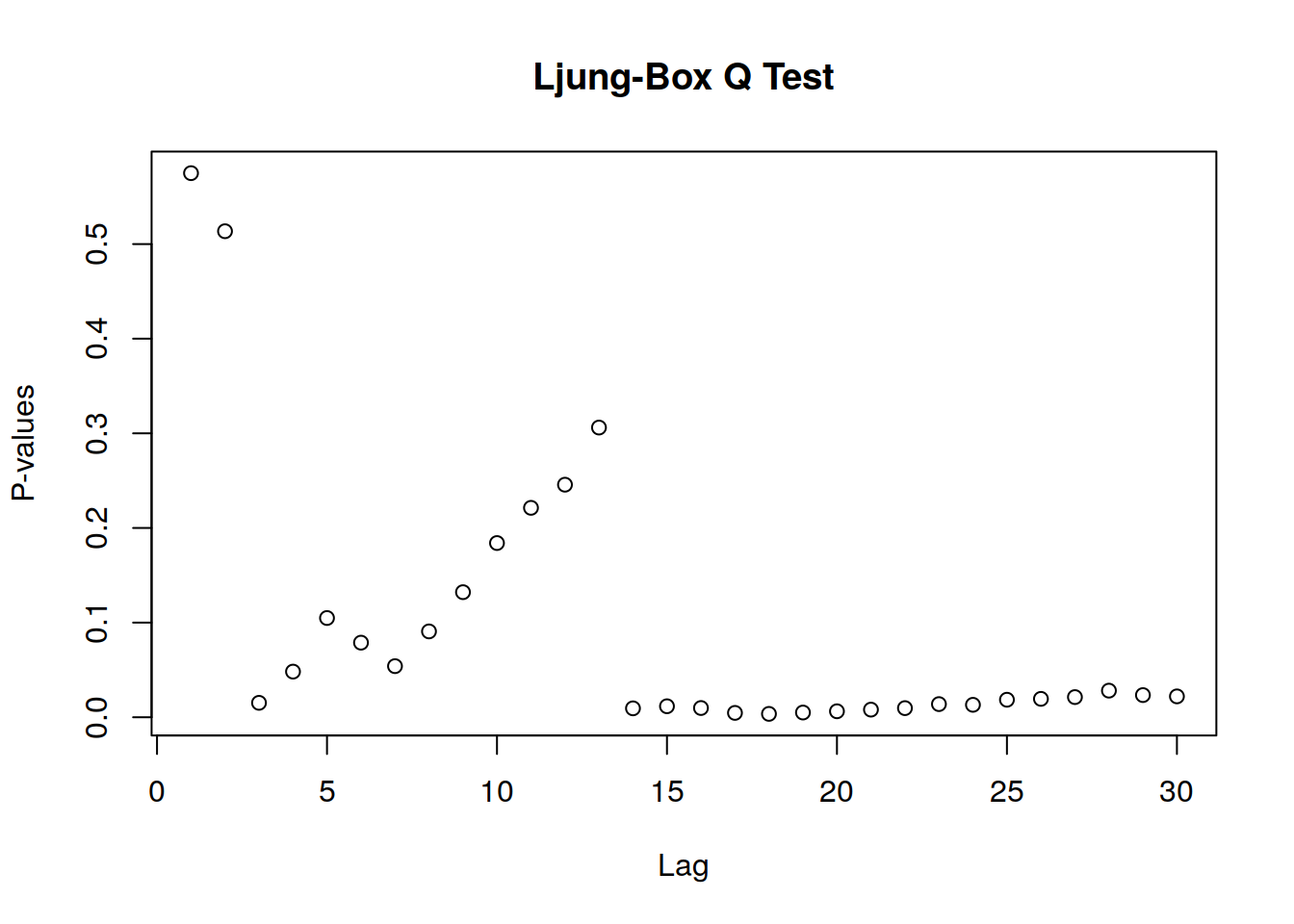
qqnorm(fitARIMA$residuals)
qqline(fitARIMA$residuals)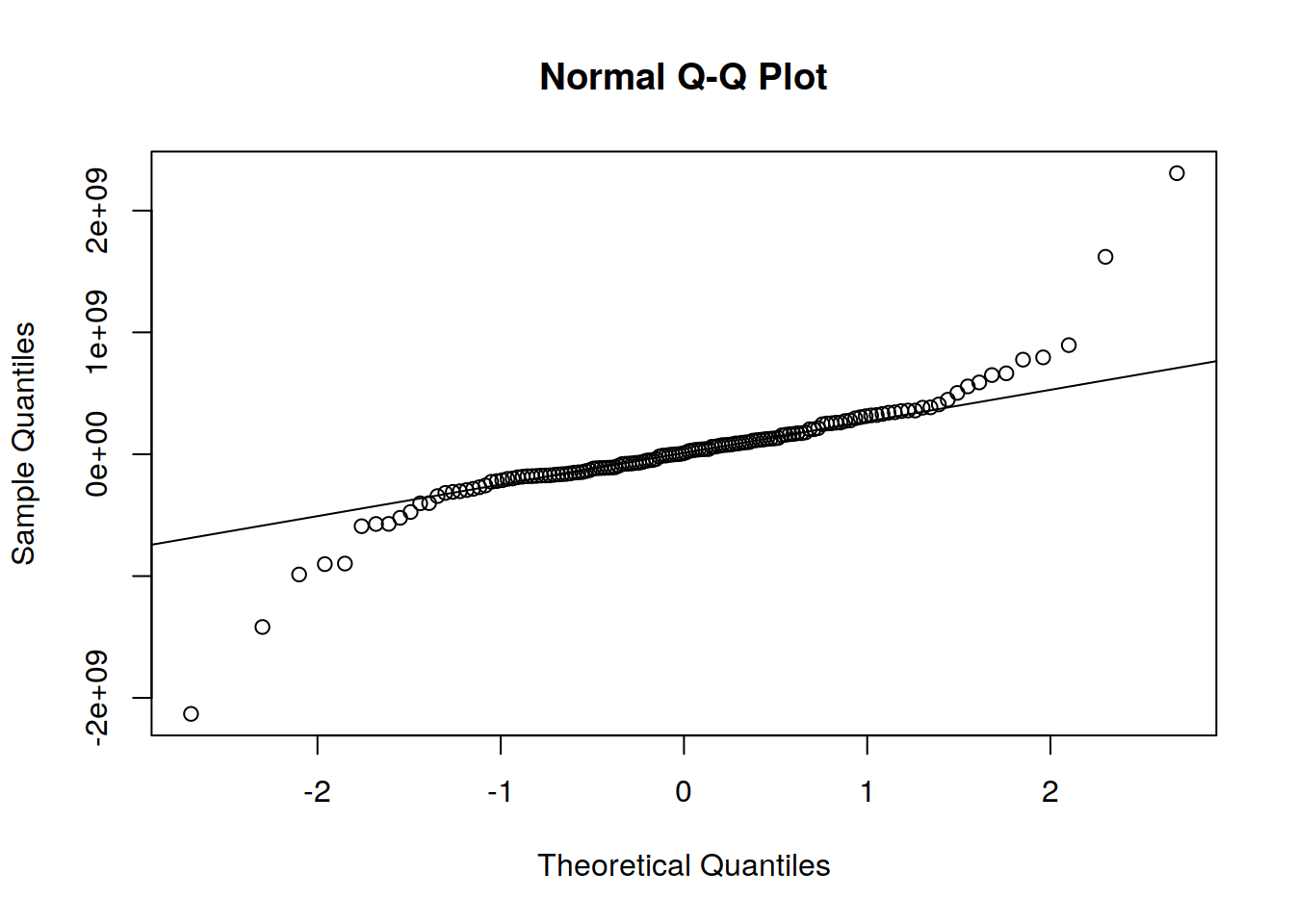
Como todos los gráficos apoyan el supuesto de que no hay un patrón en los residuales, podemos seguir adelante y calcular el pronóstico.
10.8.4 Función auto.arima ():
El paquete de pronóstico proporciona dos funciones: ets () y auto.arima () para la selección automática de modelos exponenciales y modelos ARIMA. La función auto.arima () en R utiliza una combinación de pruebas de raíz unitaria, minimización del AIC y MLE para obtener un modelo ARIMA. La prueba KPSS se usa para determinar el número de diferencias (d) En el algoritmo Hyndman- Khandakar para el modelado ARIMA automático. Los p, d y q luego se eligen minimizando el AICc. El algoritmo utiliza una búsqueda por pasos para recorrer el espacio del modelo para seleccionar el mejor modelo con el AICc más pequeño. Si d = 0, entonces se incluye la constante c; si d≥1 entonces la constante c se pone a cero. Las variaciones en el modelo actual se consideran variando p y / o q del modelo actual en ± 1 e incluyendo / excluyendo c del modelo actual. El mejor modelo considerado hasta ahora (ya sea el modelo actual o una de estas variaciones) se convierte en el nuevo modelo actual. Ahora, este proceso se repite hasta que no se pueda encontrar un AIC inferior.
#install.packages("forecast")
library(forecast)##
## Attaching package: 'forecast'## The following object is masked from 'package:FitAR':
##
## BoxCoxauto.arima(tsData, trace=TRUE)##
## ARIMA(2,1,2)(1,0,1)[12] with drift : Inf
## ARIMA(0,1,0) with drift : 5971.076
## ARIMA(1,1,0)(1,0,0)[12] with drift : Inf
## ARIMA(0,1,1)(0,0,1)[12] with drift : Inf
## ARIMA(0,1,0) : 5969.545
## ARIMA(0,1,0)(1,0,0)[12] with drift : Inf
## ARIMA(0,1,0)(0,0,1)[12] with drift : Inf
## ARIMA(0,1,0)(1,0,1)[12] with drift : Inf
## ARIMA(1,1,0) with drift : Inf
## ARIMA(0,1,1) with drift : Inf
## ARIMA(1,1,1) with drift : Inf
##
## Best model: ARIMA(0,1,0)## Series: tsData
## ARIMA(0,1,0)
##
## sigma^2 estimated as 2.586e+17: log likelihood=-2983.76
## AIC=5969.52 AICc=5969.55 BIC=5972.4510.8.5 Predecir utilizando un modelo ARIMA
Los parámetros del modelo ARIMA se pueden usar como un modelo predictivo para hacer pronósticos de valores futuros de las series temporales, una vez que se selecciona el modelo más adecuado para los datos de la serie temporal. El valor d afecta a los intervalos de predicción; los intervalos de predicción aumentan de tamaño con valores más altos de «d». Todos los intervalos de predicción serán esencialmente los mismos cuando d = 0 porque la desviación estándar de la previsión a largo plazo irá a la desviación estándar de los datos históricos. Existe una función llamada predict () que se usa para predicciones a partir de los resultados de varias funciones de ajuste de modelos. Se necesita un argumento n.ahead () que especifica la cantidad de tiempo que se adelanta para predecir.
### predict(fitARIMA,n.ahead = 5)La función forecast() en el paquete R de forecast también se puede utilizar para pronosticar valores futuros de la serie temporal. Aquí también podemos especificar el nivel de confianza para los intervalos de predicción utilizando el argumento de nivel.
futurVal <- forecast(fitARIMA,h=10, level=c(99.5))
plot(futurVal)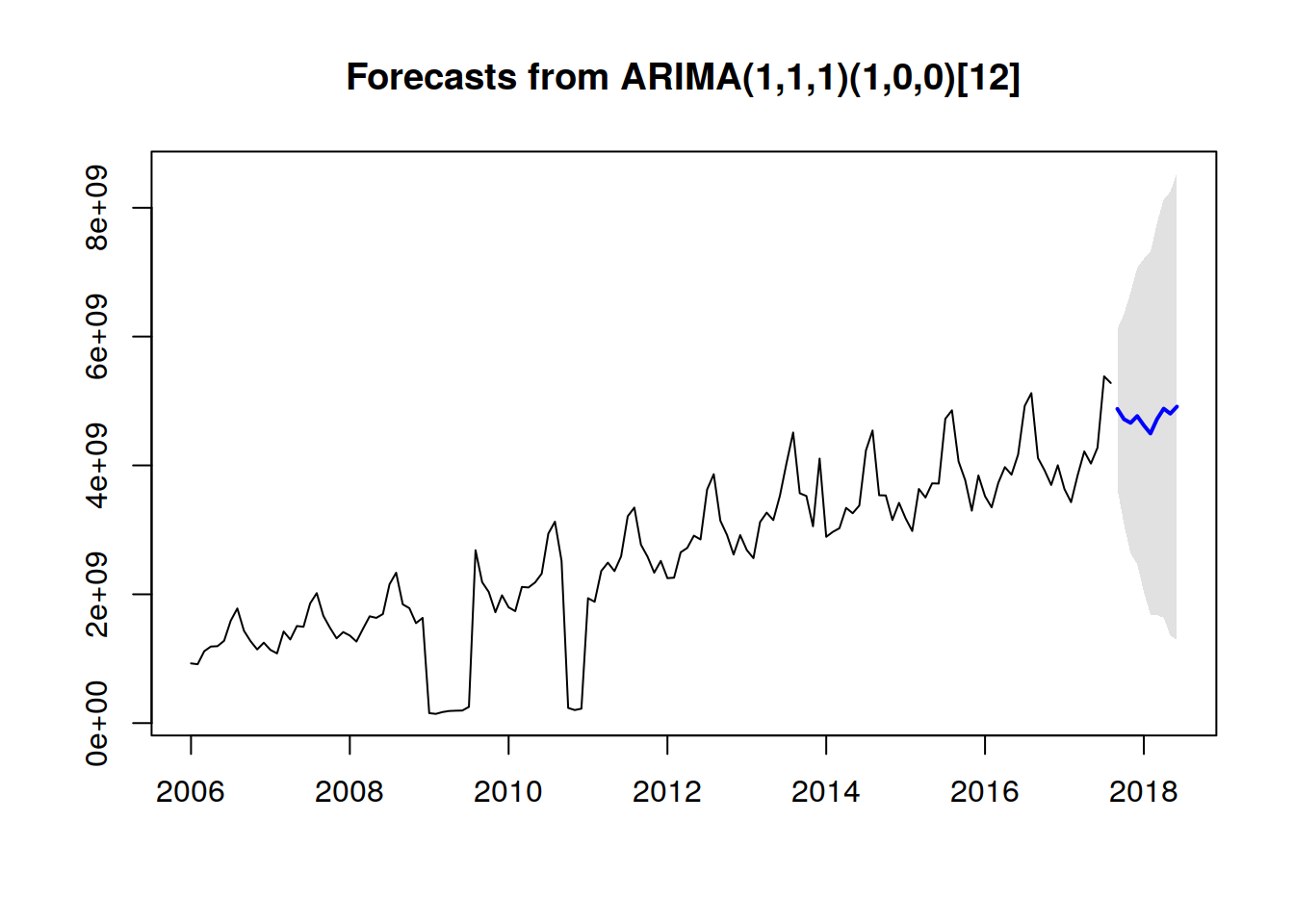
Los pronósticos se muestran como una línea azul, con los intervalos de predicción del 80% como un área sombreada oscura, y los intervalos de predicción del 95% como un área sombreada clara. Este es el proceso general analizar para analizar datos de series temporales y pronosticar valores de las series existentes utilizando ARIMA. Referencias: Time Series Analysis Using ARIMA Model In R https://datascienceplus.com/time-series-analysis-using-arima-model-in-r/