8 Scores

Si el comportamiento del componente va hacia el lado positivo, se debe interpretar como que a mayor desempeño mejor resultado o calificación. Si algún componente apunta para el lado negativo tendremos que pensar que a mayor calificación en esa dimensión pero sería el desempeño. La variable PC1 que usamos tiene mucha información valiosa. Revise todo el contenido, voy a mostrar una dimensión que es el score que indica como se comportarían todos los individuos si sólo los analizásemos con los componentes 1 y 2.

acp1 <- PC1$scores
acp1 [1:10 , ]

##          Comp.1      Comp.2      Comp.3
##  [1,] -2.684126  0.31939725  0.02791483
##  [2,] -2.714142 -0.17700123  0.21046427
##  [3,] -2.888991 -0.14494943 -0.01790026
##  [4,] -2.745343 -0.31829898 -0.03155937
##  [5,] -2.728717  0.32675451 -0.09007924
##  [6,] -2.280860  0.74133045 -0.16867766
##  [7,] -2.820538 -0.08946138 -0.25789216
##  [8,] -2.626145  0.16338496  0.02187932
##  [9,] -2.886383 -0.57831175 -0.02075957
## [10,] -2.672756 -0.11377425  0.19763272
##             Comp.4
##  [1,]  0.002262437
##  [2,]  0.099026550
##  [3,]  0.019968390
##  [4,] -0.075575817
##  [5,] -0.061258593
##  [6,] -0.024200858
##  [7,] -0.048143106
##  [8,] -0.045297871
##  [9,] -0.026744736
## [10,] -0.056295401

Voy a realizar el mismo score pero ahora solo con los componentes 1 y 2

acp2 <-PC1$scores[ ,1:2]
plot(acp2)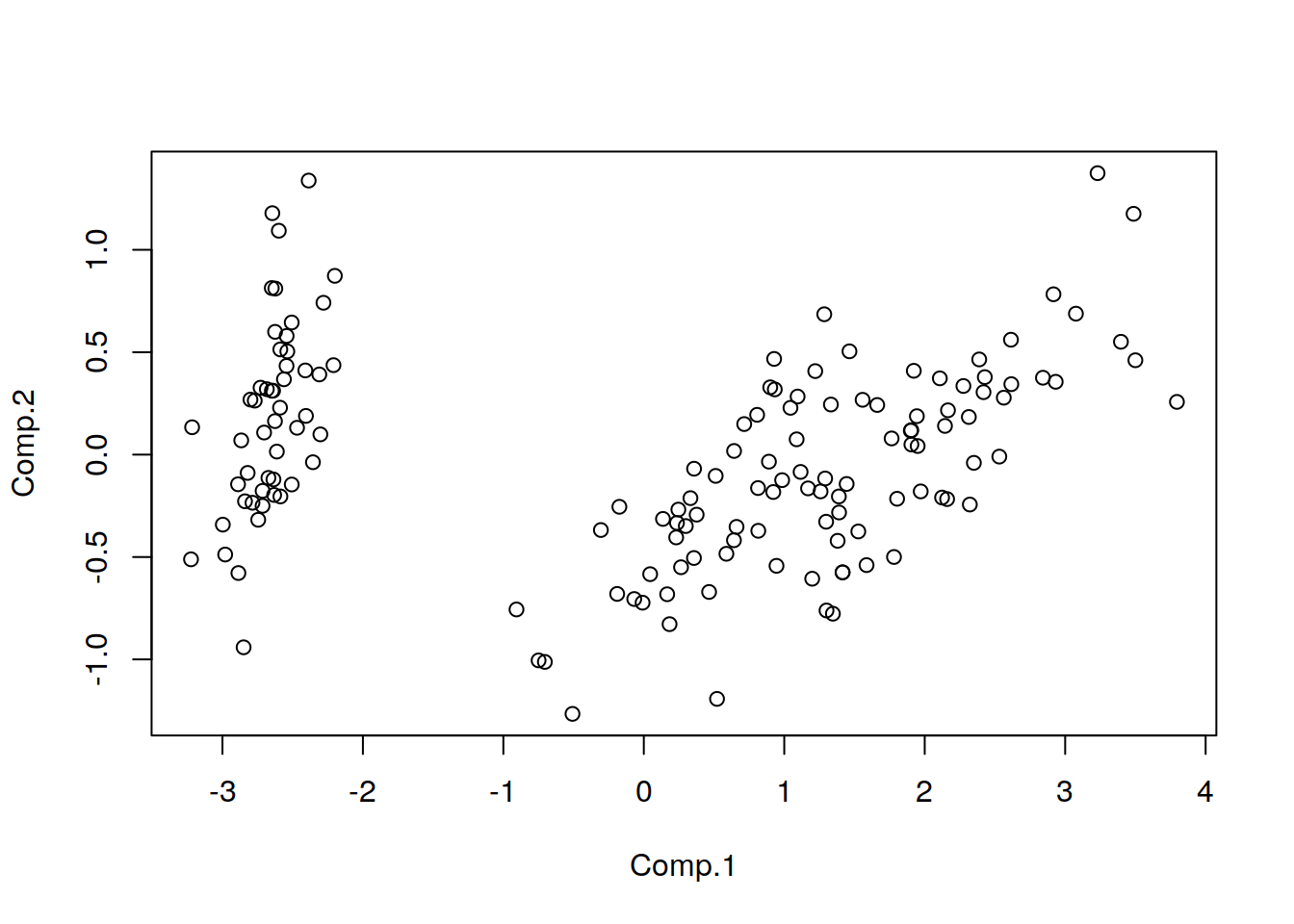

Aquí ya podemos ver más claramente la división que se produce entre distintos clusters. Para poder diferencias aún más recurriremos a un nuevo tipo de análisis diferenciado que se llama análisis de clusters

8.1 Análisis de Clusters o Conglomerados

Para realizar este análisis recurriremos a cargar la biblioteca clusters

En el análisis de conglomerados existen dos formas clásicas de estudio. Ambas recurren a las distancias euclídeas entre las muestras. Tenemos aproximaciones Jerárquicas y No Jerárquicas AGNES, CLARA, DIANA, MORA, PAM son nombres de las técnicas que la biblioteca Clusters usa. Todas las técnicas se caracterizan por ser un acrónimo de la combinación de aproximaciones que usan (Single Linkage, Complete Linkage, Average Linkage) .

Todas tienen nombre de mujer, pero esto no quiere necesariamente decir que se trate de una técnica con complicaciones inesperadas, sino más bien que si quieres lo mejor de una de ellas es mejor que la entiendas e indagues en la página del manual.

library(cluster)
agp1 = agnes(acp2,method="single")
agp2 = agnes(acp2,method="complete")
agp3 = agnes(acp2,method="average")

Con la clasificacion terminada procederemos a ver gráficamente el resultado.

par(mfrow=c(2,2))
plot(acp2)
plot(agp1)
plot(agp2)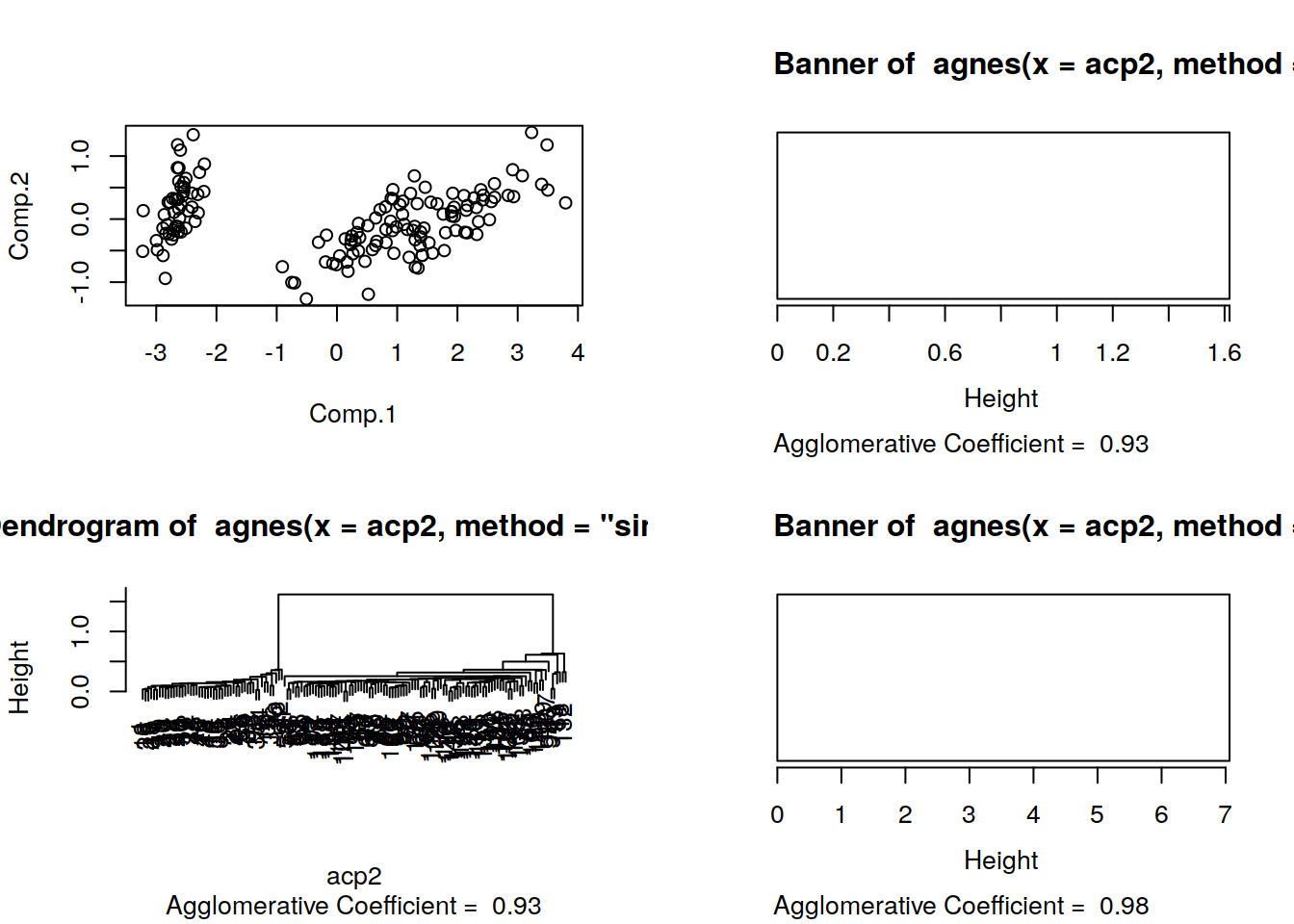

plot(agp3)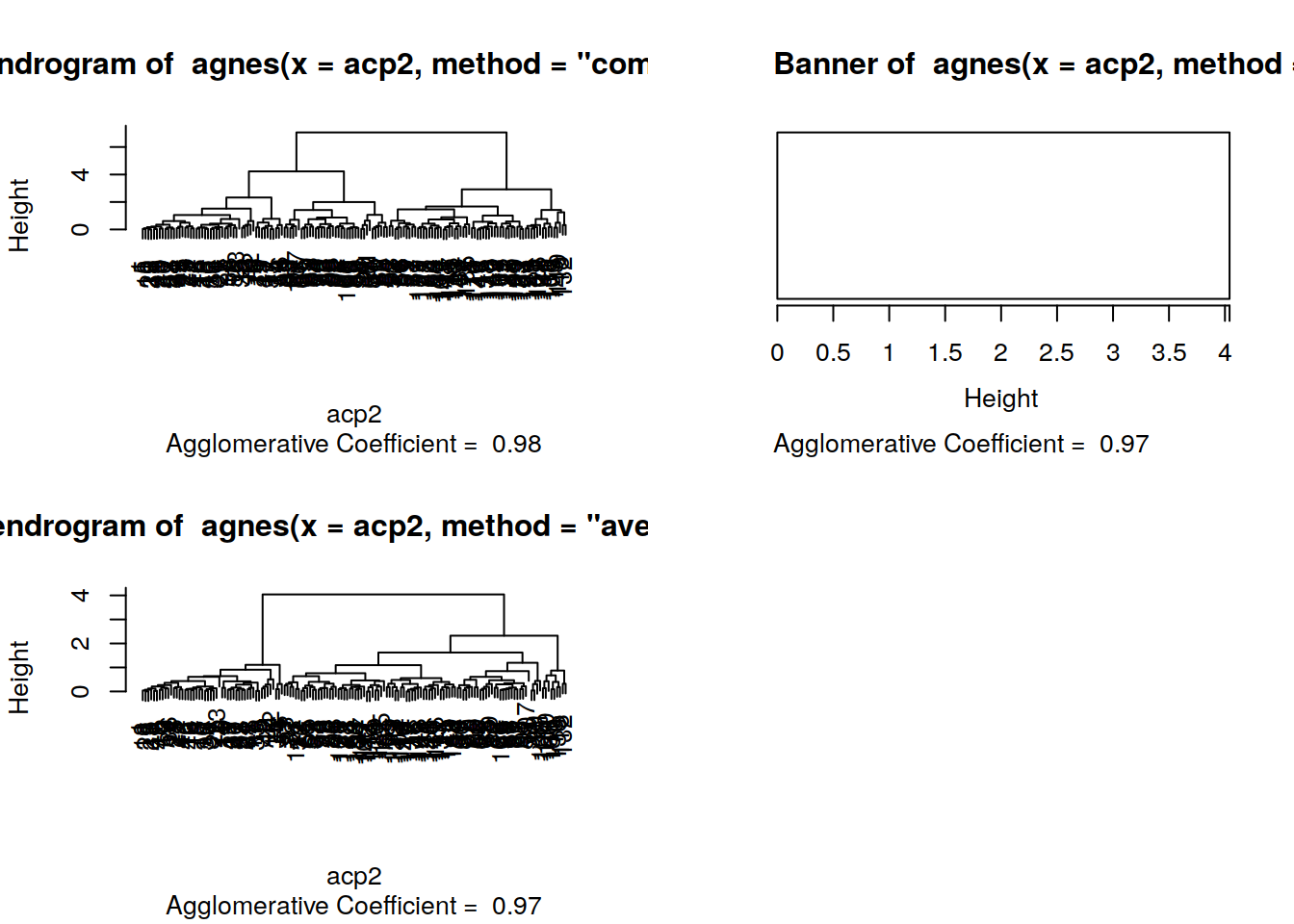

Pasa asignar las muestras a grupos usaré el comendo cuttree que me permite valerme de las franjas blancas de corte del los gráficos para armar los clusters

agpcut <- cutree(agp3,3)
par(mfrow=c(1,1))
plot(acp2,col=agpcut)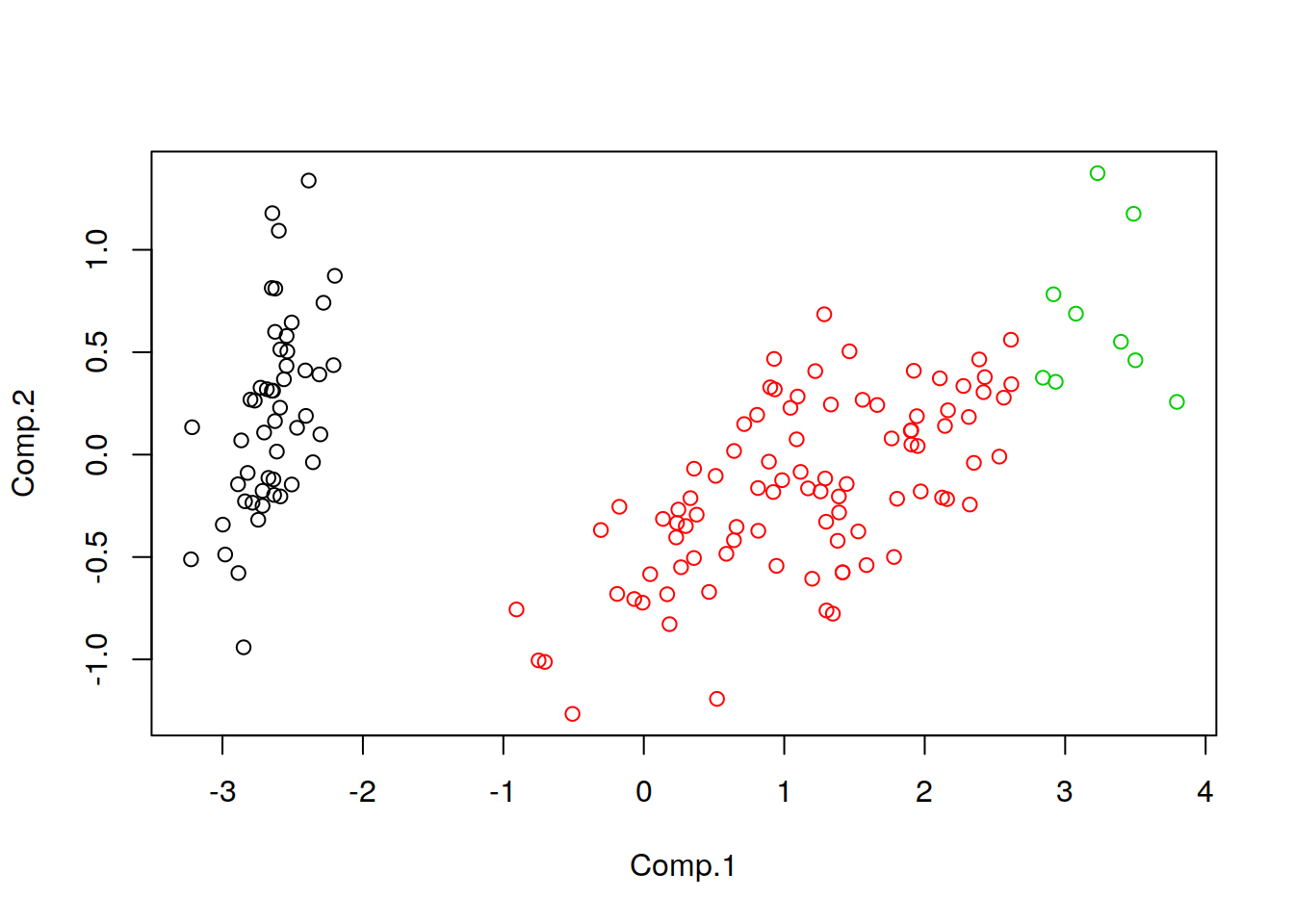

8.1.1 Otros gráficos de agrupamiento

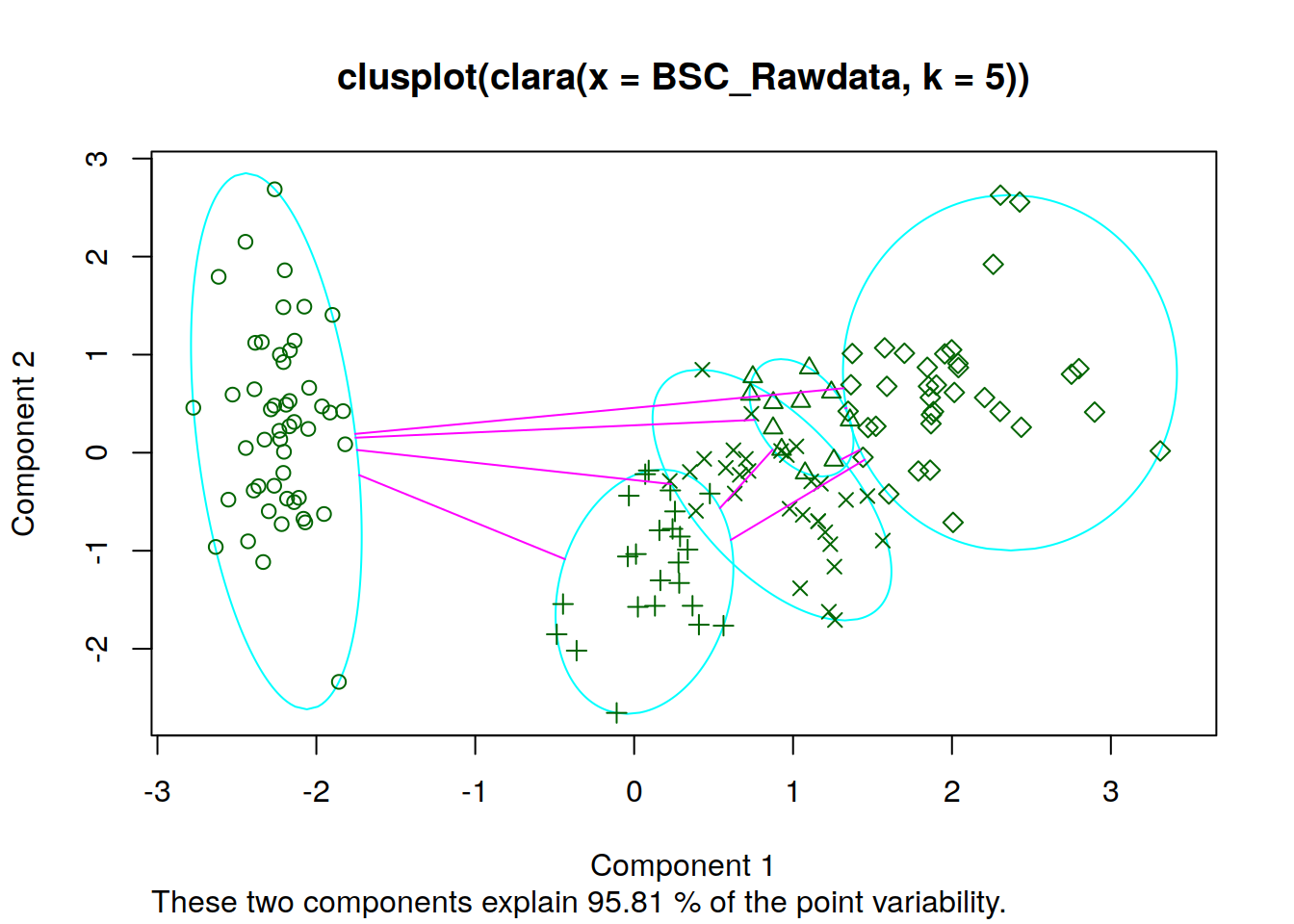
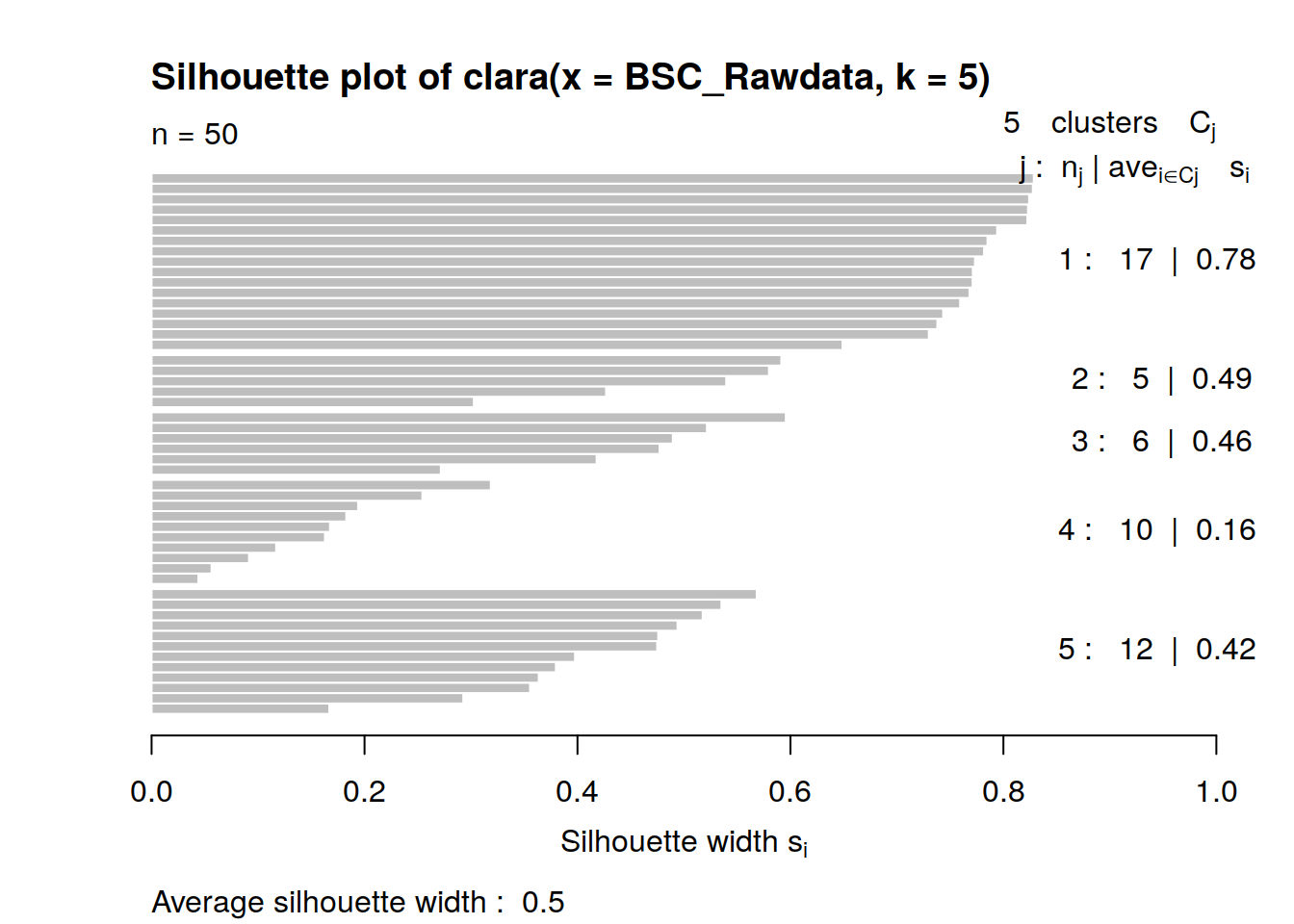
Método Clara

plot(clara(BSC_Rawdata,5))